[8주차 - Day4] 기계학습과 수학 리뷰

Deep Learning: 신경망의 기초 - 기계학습과 수학

기계학습에서 수학의 역할 : 목적함수를 정의하고 목적함수의 최저점을 찾아주는 최적화 이론 제공

최적화(optimization) 이론에 학습률(learning rate), 멈춤조건과 같은 제어를 추가하여 알고리즘 구축

1. 선형대수(linear algebra)

벡터, 즉 주어진 데이터가 어떤 공간에 존재하고 그 안에서 연산이 일어났을 때 주어져있는 공간이 어떤 영향을 미치느냐를 수학적으로 설명하는 것

1.1. 벡터와 행렬

벡터(vector) : 샘플을 특징 벡터(feature vector)로 표현

행렬(matrix) : 여러 개의 벡터를 담음

행렬을 이용하면 방정식(방정식계, system of equations)을 간결하게 표현가능 

• 설계 행렬(design matrix) : 훈련집합을 담은 행렬
• 전치 행렬(transpose matrix) : A^T
  •  
•  특수 행렬들 : 정사각행렬(정방행렬, square matrix), 대각행렬(diagonal matrix), 단위행렬(identity matrix), 대칭행렬(symmetric matrix)

행렬 연산

• 행렬 곱셈(matrix (dot) product) : 공간의 변환
  • 
  • 특성 : 교환(commutative)법칙X/분배(distributive)법칙O/결합(associatvie)법칙O
  • 행렬의 곱셈으로 생성된 각각의 요소들은 벡터의 내적으로 이루어져있음
  • 벡터의 내적(inner product) :  => 두 벡터의 유사도를 측정하는 것

    

• 행렬 덧셈 : 공간의 이동

텐서(tensor) : 3차원 이상의 구조를 가진 숫자 배열(array)   ex)RGB

1.2. 놈과 유사도

벡터와 행렬의 거리(크기)를 놈(norm)으로 측정

• 벡터의 p차 놈

  

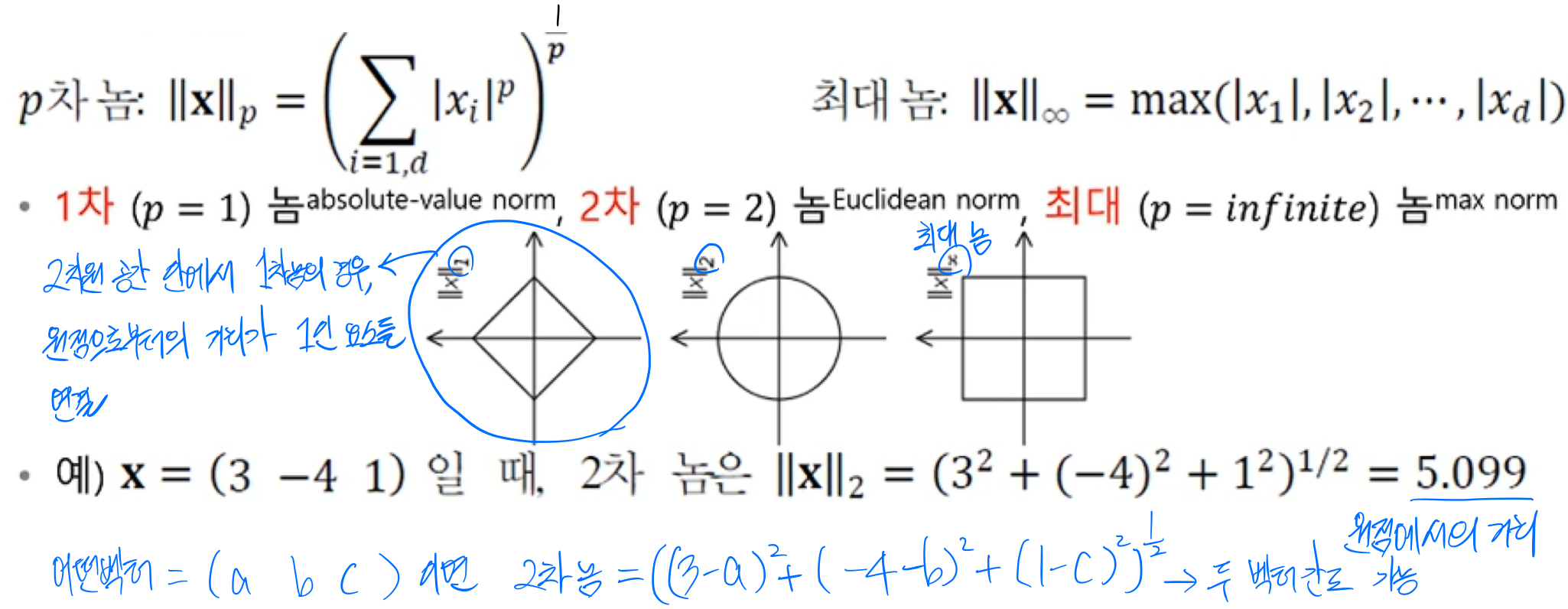
• 행렬의 프로베니우스 놈(Frobenius norm) : 행렬의 크기를 측정

  

놈을 어따가 쓰느냐 하면 하강 기울기의 규제의 경우에 사용

1.3. 퍼셉트론(perceptron)의 해석

퍼셉트론 : 분류기(classifier)모델

퍼셉트론의 동작을 수식으로 표현한 것

퍼셉트론의 물리적 의미 : 2차원에선 결정직선(decision lines), 3차원에선 결정평면(decision plane), 4차원에선 결정 초평면(decision hyperplane) 즉, 공간을 분류하는 기준이 됨

multilayer perceptron : 퍼셉트론 각각의 가중치가 있어야함

학습의 정의

• 추론(inferring) : 학습을 마친 알고리즘을 현장의 새로운 데이터에 적용하는 작업->분류
• 훈련(training): 훈련집합의 샘플에 대해 퍼센트론 수식을 가장 잘 만족하는 w를 찾아내는 작업->학습

1.4. 선형결합과 벡터공간

벡터 : 공간상의 한점으로 끝이 벡터의 좌표에 해당

벡터공간(vector space) : 기저(basis)벡터 a와 b의 선형결합(linear combination)으로 만들어지는 공간

1.5. 역행렬(matrix inversion)

원래 벡터에 행렬의 연산에 의해 변화를 한 벡터를 원상복구시켜주는 것

특징

1. 행렬식이 0이 아님
   • 행렬 A의 행렬식(determinant)=det(A)
   • 행렬식은 주어진 행렬의 곱에 의한 공간의 확장 또는 축소 해석
     • det(A)=0, 하나의 차원을 따라 축소되어 부피를 잃게 됨
     • det(A)=1, 부피 유지한 변환/방향 보존O
     • det(A)=-1, 부피 유지한 변환/방향 보존X
       

       

       왼쪽은 5배 부피 확장, 방향 보존O

2. A^T*A는 양의 정부호(positive definite)대칭 행렬
   • 정부호(definiteness)행렬 : 행렬의 공간이 어떻게 생겼는지 확인할 때 사용
     • 양의 정부호 행렬 : 0이 아닌 모든 벡터 x에 대해 x^T*A*x>0

       

       • 성질 : 고유값 모두 양수/역행렬도 정부호 행렬/det(A)!=0 즉, 역행렬 존재
     • 양의 준정부호(positive semi-definite)행렬 : 0이 아닌 모든 벡터 x에 대해 x^T*A*x>=0
     • 음의 정부호(negative definite)행렬 : 0이 아닌 모든 벡터 x에 대해 x^T*A*x<0
     • 음의 준정부호(negative semi-definite)행렬 : 0이 아닌 모든 벡터 x에 대해 x^T*A*x<=0

1.6. 행렬 분해(matrix decomposition)

고윳값(eigenvalue)와 고유벡터(eigenvector)

Av=λv : 고유 벡터 v와 고윳값 λ

고유 벡터 방향으로는 고유값만큼 크기만 변환!

고유 분해(eigen-decomposition)

고유 분해

고유 분해는 고유값과 해당 고유벡터가 존재하는 정사각행렬에만 적용 가능

그래서 나온 게 특잇값행렬(SVD, Singular value decomposition)!

특이값 분해

특이값 분해의 기하학적 해석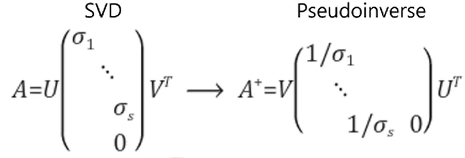

정사각행렬이 아닌 행렬의 역행렬 계산에 사용

2. 확률과 통계

기계학습이 처리할 데이터는 불확실한 세상에서 발생하므로 불확실성(uncertainty)을 다루는 확률과 통계를 잘 활용

2.1. 확률 기초

확률변수(random variable)와 확률변수의 정의역(domain)

확률 분포(probability distribution)

• 확률질량함수(probability mass funtion) : 이산(discrete) 확률 변수
• 확률밀도함수(probability density function) : 연속(continuous) 확률 변수

확률벡터(random vector) : 확률 변수를 요소로 가짐

ex)Iris에서 X는 4차원 확률 벡터 X=(x1, x2, x3, x4)^T=(꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비)^T

확률 규칙

2.2. 베이즈 정리와 기계 학습

베이즈 정리(Bayes's rule)

ex)하얀 공이 나왔다는 사실만 알고 어느 병에서 나왔는지 모르는데 어느 병인지 추정

x : 공 / y : 병

(x : 공, y : 병)

 

->x(어떤 공)가 주어졌을 때 y(어떤 병)가 발현되는 확률을 가장 크게 만들어주는 argument y를 찾아라

베이즈 정리의 해석 : 사후(posteriori) 확률 = 우도(likelihood) 확률 * 사전(prior) 확률

확률과 우도

• 확률 : 어떤 분포에서부터 우리가 가질 수 있는 모든 숫자들을 정형화
• 우도 : 확률의 분포로부터 데이터를 생성해서 유추, 관찰된 값에서부터 나오는 것, 관심있는 대상에 대해서 데이터 샘플을 취해서 확률분포를 유추

사후확률P(y|x)을 직접 추정하는 일은 불가능->베이즈 정리를 이용하여 추정

2.3. 최대 우도(ML, Maximum likelihood)

매개변수(모수, parameter)를 모르는 상황에서 매개변수를 추정하는 문제

어떤 확률변수의 관찰된 값들을 토대로 그 확률변수의 매개변수를 구하는 방법

최대우도추정

최대우도추정

눈에 보이지 않는 θ에서 데이터 X가 발현되는데

X를 보고 θ를 설명하는 likelihood를 maximize

->최대우도

최대 로그우도 추정

곱->합으로 계산 단순화하기 위해 로그 사용

 

확률분포를 설명하기 위해 내가 가지고 있는 데이터로 설명하겠다 만드는 것->우도

우도를 통해 알고싶어하는 대상의 확률을 설명할 수 있는 모수의 매개변수를 알고자하는 것->최대우도

2.4. 평균과 분산

데이터의 요약정보

분산 : 데이터들이 평균에서 얼마나 멀리에 분포해있는지, 데이터가 어떻게 퍼져있는지

우리가 보는 건 다차원이기 때문에 평균 벡터(치우침 정도)를 봐야함

공분산 행렬(covariance matrix) : 확률변수의 상관정도, 차원과 차원간의 관계, 차원들간의 데이터 퍼짐이나 상관도

평균벡터와 공분산 행렬

2.5. 유용한 확률분포

가우시안 분포(Gaussian distribution)

베르누이 분포(Bernoulli distribution)

성공(x=1)확률이 p이고 실패(x=0)의 확률이 1-p인 분포

이항분포(Binomial distribution)

성공 확률이 p인 베르누이 실험을 m번 수행할 때 성공할 횟수의 확률 분포

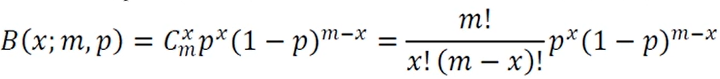
지수분포(exponential distribution)

라플라스 분포(Laplace distribution)

디랙 분포(Dirac distribution)

혼합 분포들(Mixture distribution)

여러 분포들을 사용해서 설명(대신 하나의 종류만)

3개의 가우시안 분포

확률 분포와 연관된 유용한 함수들

• 로지스틱 시그모이드 함수(logistic sigmoid function)
  • 활성함수의 대표적 함수, 비선형
  • 일반적으로 베르누이 분포의 매개변수를 조정을 통해 얻어짐
  • 주어져있는 x값으로 y값을 0~1사이로 만들어주는 함수
  •  

    

• 소프트플러스 함수(softplus function)
  • 활성함수의 대표적 함수, 비선형
  • 정규분포의 매개변수의 조정을 통해 얻어짐

  • 

변수 변환(change of variables)

기존 확률변수를 새로운 확률 변수로 바꾸는 것

변수변환예시

2.6. 정보이론

확률통계는 해당 확률 분포를 추정하고 확률 분포 간의 유사성을 정량화

정보이론은 불확실성을 정량화하여 기계학습에 활용

정보이론 : 사건(event)이 지닌 정보를 정량화

정보이론의 기본 원리 : 확률이 작을수록 많은 정보, 자주 발생하는 사건보다 잘 일어나지 않는 사건(unlikely event)의 정보량(informative)이 많음

자기정보(self information) : 사건(메시지)의 정보량

해당하는 이벤트가 얼마만큼의 확률을 가지고 있는지, 확률변수 1개에 대해서 정보를 측정하는 것

로그 밑이 2면 bit(비트)/자연상수(e)이면 nat(나츠)

ex)동전에서 앞면이 나오는 사건의 정보량 : -log (1/2)=1

    주사위에서 1이 나오느 사건의 정보량 : -log (1/6)=2.58

->후자의 사건이 전자의 사건보다 높은 정보량을 가짐

얼마만큼의 정보를 많이 담아 보낼 수 있는지 정보의 손실이 없게 보낼 수 있는지의 척도가 됨

엔트로피(entropy) : 확률변수 x의 불확실성을 나타내는 엔트로피

x가 가질 수 있는 모든 사건의 불확실성을 정량화, 모든 사건 정보량의 기대 값으로 표현

이산확률분포

연속확률분포 : 연속이기 때문에 적분을 통해서 확률값 얻을 수 있음

해당하는 확률변수가 가질 수 있는 모든 이벤트들의 자기 정보를 다 더한 기댓값

해당하는 확률변수가 얼마만큼의 정보량을 가질 수 있느냐의 지표

ex1)동전의 앞뒤 발생 확률이 동일한 경우 엔트로피

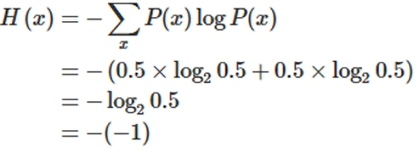
ex2)동전 발생 확률에 따른 엔트로피 변화

알 수 있는 것

1. 엔트로피의 최대값이 1->결과 전송시 최대 1비트 필요

2. 가장 큰 엔트로피를 가질 때 : 앞이 나올 확률=뒤가 나올 확률

    ->모든 사건이 동일한 확률일 때, 

       즉, 불확실성이 가장 높은 경우 엔트로피가 최대!

 

 

ex3)윷과 주사위의 엔트로피

윷의 엔트로피

주사위의 엔트로피

주사위가 윷보다 엔트로피가 높은 이유 : 주사위는 모든 사건이 동일한 확률을 갖고 있기 때문에 어떤 사건이 일어날 지 윷보다 예측이 어려움->주사위가 윷보다 무질서하고 불확실성이 큼->엔트로피가 큼!

교차 엔트로피(cross entropy) : 두 확률분포 P와 Q사이의 교차 엔트로피

엔트로피는 하나의 random variable에 대해서 불확실성을 정량화시켜서 정보화

확률분포 2개를 가지고 서로가 정보를 얼마나 공유하고있는지가 교차 엔트로피

교차 엔트로피는 심층학습(deep learning)의 손실함수로 사용됨

• 정답(실제값)과 예측값을 비교하는게 손실함수
• 손실함수 관점에서 봤을 때 두 개를 비교해봤을 때 얼마만큼 멀리 떨어져있느냐
• 예측값과 실제값 둘 다 확률 분포기 때문에 손실함수로 많이 사용

교차 엔트로피 식의 전개

P : 데이터가 만드는 분포 /Q : 어떤 대상

->P는 데이터 분포기 때문에 변화가 없음, 교차 엔트로피를 손실함수로 사용하면(손실함수는 최소화시키는 것이 목적) H(P)는 P에 대한 식이므로 변화가 없고 움직일 수 있는 대상인 Q(x)가 있는 KL발산을 최소화시키는 것이 목표가 됨

그럼 KL발산(divergence)란?

두 확률 분포 사이의 거리를 계산할 때 주로 사용

즉, 가지고 있는 데이터 분포 P(x)와 추정한 데이터 분포 Q(x)간의 차이를 최소화시키는데 교차 엔트로피 사용

3. 최적화

기계학습의 최적화는 훈련집합이 주어지고 훈련집합에 따라 정해지는 목적함수의 최저점으로 만드는 모델의 매개변수를 찾아야함

주로 SGD(확률론적 경사 하강법,Stochastic Gradient Descent)사용

손실함수 미분하는 과정이 필요->오류 역전파(backpropagation)알고리즘

3.1. 매개변수 공간의 탐색

차원에 비해 훈련집합의 크기가 작아 참인 확률분포를 구하는 일은 불가능

->적절한 모델(가설)을 선택, 목적함수를 정의, 모델의 매개변수 공간을 탐색하여 목적함수가 최저가 되는 최적점을 찾는 전략 사용 즉, 특징 공간(차원)에서 해야할 일을 모델의 매개변수 공간에서 하는 일로 대체!

학습 모델의 매개변수 공간은 특징 공간보다 많은 차원을 가짐

최적화 문제 해결 방법

• 낱낱탐색(exhaustive search) 알고리즘
• 무작위탐색(random search) 알고리즘
• 기계학습이 사용하는 전형적인 탐색 알고리즘
  • 목적함수가 작아지는 방향을 주로 미분(gradient)으로 찾아냄

3.2. 미분

미분에 의한 최적화?

1차 도함수 f'(x)는 함수의 기울기(경사)=값이 커지는 방향임->-f'(x)방향에 목적함수의 최저점이 존재할 것

편미분(partial derivative) : 변수가 복수인 함수의 미분

미분 값이 이루는 벡터를 경사도(변화도, gradient)라고 부름

gradient의 여러가지 표기

독립변수와 종속변수의 구분

일반적으로 y=wx+b

x는 독립변수, y는 종속 변수

기계학습의 관점에서 보면 최적화는 예측 단계가 아닌 학습 단계에서 필요

손실함수

θ가 독립변수, error=J(θ)라 하면 error가 종속변수

θ를 잘 탐색해서 J값(error)을 낮추는 과정을 최적화를 통해 수행할 것

연쇄법칙(chain rule)

합성함수 f(x)=g(h(x)), f(x)=g(h(i(x)))의 미분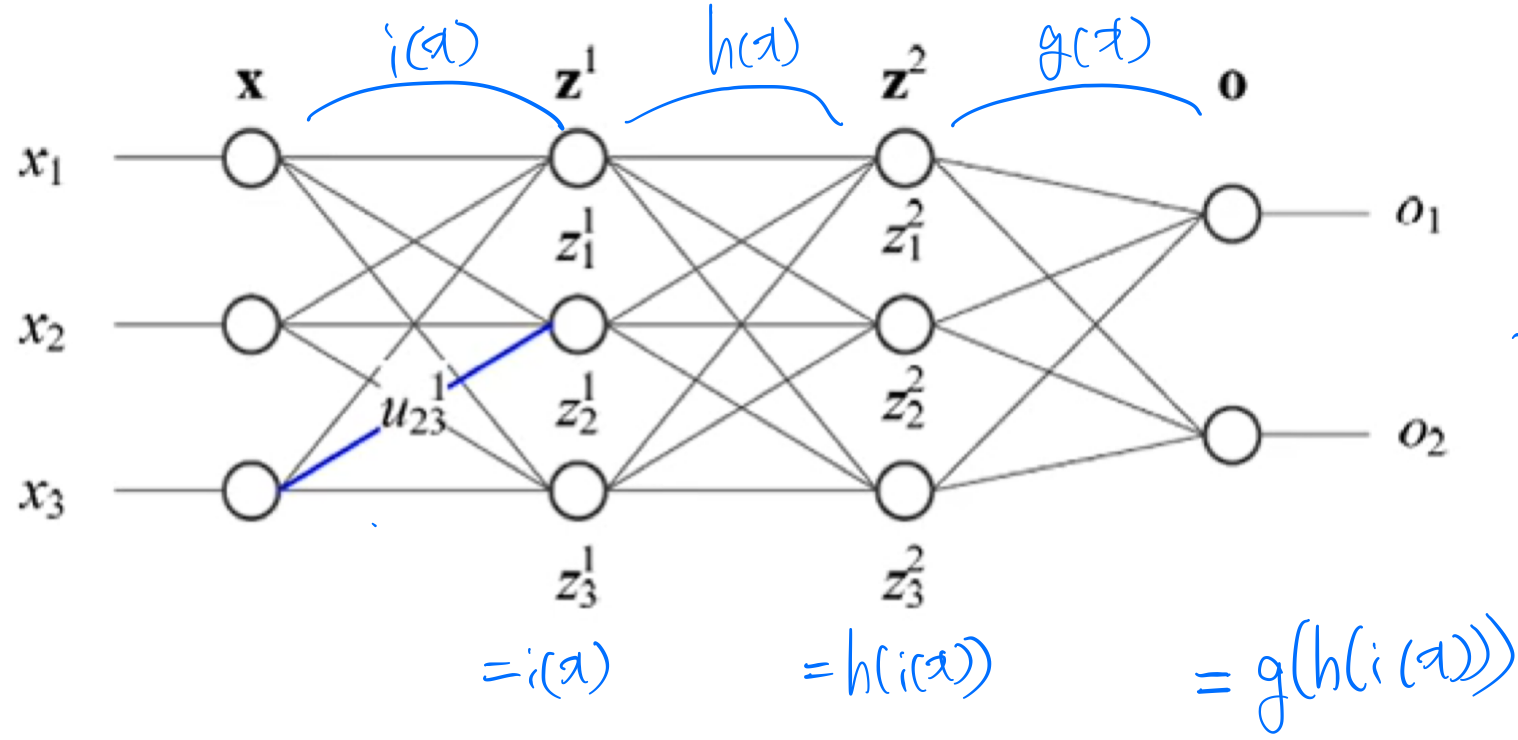

다층 퍼셉트론은 합성함수

야코비언 행렬(jacobian matrix) : 행렬을 1차 미분

헤세 행렬(Hessian matrix) : 행렬을 2차 미분

3.3. 경사 하강 알고리즘

함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 반복적으로 이동하여 최소값에 도달하도록 하는 알고리즘

• 집단(무리, batch) 경사 하강 알고리즘(BGD) : 샘플의 경사도를 구하고 평균한 후 한꺼번에 갱신, 정확하지만 느림
• 확률론적 경사 하강 알고리즘(SGD) : 한 샘플 혹은 작은 집단(mini batch)의 경사도를 계산한 후 즉시 갱신, 빠르지만 다소 헤맬 수 있음
• 추가 경사 하강 알고리즘 : Momentum, NAG, Adagrad, Adadelta, Rmsprop

 

Deep Learning: 신경망의 기초 - 실습I

GPU는 병렬 계산에 유리하므로 행렬의 계산을 CPU보다 효율적으로 할 수 있음

이 연산그래프를 numpy로 gradient계산하면 아래와 같은 코드

import numpy as np
np.random.seed(0)

N,D=3,4
x=np.random.randn(N,D)
y=np.random.randn(N,D)
z=np.random.randn(N,D)

a=x*y
b=a+z
c=np.sum(b)

grad_c=1.0
grad_b=grad_c*np.ones((N,D))
grad_a=grad_b.copy()
grad_z=grad_b.copy()
grad_x=grad_a*y
grad_y=grad_a*x

#PyTorch에선 requires_grad=True설정, backward()로 gradient 자동 계산
import torch

N,D=3,4
x=torch.randn(N,D, requires_grad=True)
y=torch.randn(N,D)
z=torch.randn(N,D)

a=x*y
b=a+z
c=torch.sum(b)

c.backward()
print(x.grad)

#gpu사용
import torch

device='cuda:0'
N,D=3,4
x=torch.randn(N,D, requires_grad=True, device=device)
y=torch.randn(N,D, device=device)
z=torch.randn(N,D, device=device)

a=x*y
b=a+z
c=torch.sum(b)

c.backward()
print(x.grad)

PyTorch

PyTorch특징

• tensor : numpy array와 비슷한데 GPU연산가능
• autograd : tensor를 이용해서 연산 그래프를 쌓고 자동으로 gradients를 계산해주는 패키지
• module : neural network layer

예제)two-layer ReLU network on random data with L2 loss

1. PyTorch : Tensors

import torch

device=torch.device('cuda:0')

N,D_in, H, D_out=64, 1000, 100, 10
#입력값
x=torch.randn(N,D_in, device=device)
y=torch.randn(N,D_out, device=device)
#가중치
w1=torch.randn(D_in, H, device=device)
w2=torch.randn(H, D_out, device=device)

learning_rate=1e-6
for t in range(500):
    #forward pass : predictions,loss 계산
    h=x.mm(w1)	#torch.mm()->행렬곱
    h_relu=h.clamp(min=0)	#torch.clamp()->원하는 범위로 변경, 여기선 0보다 크거나 같도록
    y_pred=h_relu.mm(w2)
    loss=(y_pred-y).pow(2).sum()

    #backward pass : gradients 계산
    grad_y_pred=2.0*(y_pred-y)
    grad_w2=h_relu.t().mm(grad_y_pred)	#torch.t()->전치 행렬
    grad_h_relu=grad_y_pred.mm(w2.t())
    grad_h=grad_h_relu.clone()
    grad_h[h<0]=0
    grad_w1=x.t().mm(grad_h)

    #gradient를 통해 가중치 갱신
    w1-=learning_rate*grad_w1
    w2-=learning_rate*grad_w2

2. PyTorch : autograd

import torch

N,D_in, H, D_out=64, 1000, 100, 10
#입력값, 정답값이라서 학습이 필요X->gradients도 필요X라서 requires_grad를 따로 설정X
x=torch.randn(N, D_in)
y=torch.randn(N,D_out)
#가중치값이라서 학습이 필요O->gradients도 필요O
#requires_grad=True를 통해 자동으로 gradients계산(autograd)
w1=torch.randn(D_in, H, requires_grad=True)
w2=torch.randn(H, D_out, reuqires_grad=True)

learning_rate=1e-6
for t in range(500):
    #forward pass
    #PyTorch가 중간값들을 자동으로 저장하기 때문에 따로 설정할 필요X
    y_pred=x.mm(w1).clamp(min=0).mm(w2)
    loss=(y_pred-y).pow(2).sum()

    #backward pass
    #gradients자동계산
    loss.backward()

    #gradients를 통해 가중치 갱신
    with torch.no_grad():   #연산 그래프를 필요로 하지 않음=gradient를 추적할 필요없다
        w1-=learning_rate*w1.grad
        w2-=learning_rate*w2.grad
        w1.grad.zero_()
        w2.grad.zero_()

3. PyTorch : nn

import torch

N,D_in, H, D_out=64, 1000, 100, 10
x=torch.randn(N, D_in)
y=torch.randn(N,D_out)

#모델 선언, 각각의 모델이 학습할 수 있는 가중치를 가지고 있음
model=torch.nn.Sequential(
    torch.nn.Linear(D_in,H),
    torch.nn.ReLU(),
    torch.nn.Linear(H, D_out)
)

learning_rate=1e-2
#forward pass : 모델에 데이터를 넣어서 loss계산
for t in range(500):
    y_pred=model(x)
    loss=torch.nn.functional.mse_loss(y_pred, y)

    #backward pass
    loss.backward()

    with torch.no_grad():   #연산 그래프를 필요로 하지 않음=gradient를 추적할 필요없다
        #모델의 파라미터들을 학습
        for param in model.parameters():
            param-=learning_rate*param.grad
    model.zero_grad()

4. PyTorch : optim

import torch

N,D_in, H, D_out=64, 1000, 100, 10
x=torch.randn(N, D_in)
y=torch.randn(N,D_out)

#모델 선언, 각각의 모델이 학습할 수 있는 가중치를 가지고 있음
model=torch.nn.Sequential(
    torch.nn.Linear(D_in,H),
    torch.nn.ReLU(),
    torch.nn.Linear(H, D_out)
)

learning_rate=1e-4
#Adam이라는 optimizer를 통해 해당 모델 파라미터를 학습시키겠다
optimizer=torch.optim.Adam(model.paramters(), lr=learning_rate)
#forward pass : 모델에 데이터를 넣어서 loss계산
for t in range(500):
    y_pred=model(x)
    loss=torch.nn.functional.mse_loss(y_pred, y)

    #backward pass, gradient계산
    loss.backward()

    #model.parameters()에 있는 gradient를 통해 학습을 시킴
    optimizer.step()
    #gradient초기화 안하면 누적되게 구현되어 있음
    optimizer.zero_grad()

5. PyTorch : DataLoaders

import torch
from torch.utils.data import TensorDataset, DataLoader

class TwoLayerNet(torch.nn.Module):
    def __init__(self, D_in, H, D_out):
        super(TwoLayerNet, self).__init__()
        self.linear1=torch.nn.Linear(D_in, H)
        self.linear2 = torch.nn.Linear(H, D_out)

    def forward(self, x):
        h_relu=self.linear1(x).clamp(min=0)
        y_pred=self.linear2(h_relu)
        return y_pred

N,D_in, H, D_out=64, 1000, 100, 10
x=torch.randn(N, D_in)
y=torch.randn(N,D_out)

#dataloader : dataset을 wrapping해서 batch단위나 shuffle할건지등 설정
loader=DataLoader(TensorDataset(x,y), batch_size=8)
model=TwoLayerNet(D_in, H, D_out)

optimizer=torch.optim.SGD(model.paramters(), lr=1e-2)
#forward pass : 모델에 데이터를 넣어서 loss계산
for epoch in range(20):
    #for문을 돌면서 batch가 하나씩 나오는데 이 때 8개씩 갖고있는 mini batch단위
    for x_batch, y_batch in loader:
        y_pred = model(x_batch)
        loss=torch.nn.functional.mse_loss(y_pred, y_batch)

        loss.backward()

        optimizer.ste()
        optimizer.zero_grad()

6. PyTorch : Pretrained Models

import torch
#torchvision : 기존에 많이 사용되는 모델들의 가중치를 다운받아서 사용할 수 있도록하는 패키지
import torchvision

alexnet=torchvision.models.alexnet(pretrained=True)
vgg16=torchvision.models.vgg16(pretrained=True)
resnet101=torchvision.models.resnet101(pretrained=True)

7. PyTorch : Visdom

visualization tool

 

8. PyTorch : tensorboard X

tensorflow 웹기반 visualization tool

 

9. PyTorch : Dynamic Computation Graphs

연산을 하면서 그래프를 쌓음 연산이 끝나면 그래프 버림 비효율적으로 보일수도 있음

import torch

N,D_in, H, D_out=64, 1000, 100, 10
x=torch.randn(N,D_in)
y=torch.randn(N, D_out)
w1=torch.randn(D_in, H, requires_grad=True)
w2=torch.randn(H,D_out, requires_grad=True)

learning_rate=1e-6
for t in range(500):
    y_pred=x.mm(w1).clamp(min=0).mm(w2)
    loss=(y_pred-y).pow(2).sum()

    loss.backward()

+Static Computation Graphs

먼저 그래프를 쌓고 연산이 끝나도 버리지 않고 계속 사용

graph=build_graph()

for x_batch, y_batch in loader:
	run_graph(graph, x=x_batch, y=y_batch)

->tensorflow 2.0 버전 이전에 주로 사용되었음

dynamic computation graph를 사용하면 코드가 간결해짐

TensorFlow

1. TensorFlow : Neural Net

import tensorflow as tf
import numpy as np
N, D, H=64, 1000, 100

#tensorflow는 TF tensor를 사용하는데 이는 numpy array를 변환해서도 생성가능
x=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
y=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
w1=tf.Variable(tf.random.uniform((D,H)))
w2=tf.Variable(tf.random.uniform((H,D)))

#tf.GraidentTape()를 이용하여 Dynamic computational graph 쌓기가능
with tf.GradientTape() as tape:
    #forward pass
    h=tf.maximum(tf.matmul(x,w1),0)
    y_pred=tf.matmul(h,w2)
    diff=y_pred-y
    loss=tf.reduce_mean(tf.reduce_sum(diff**2, axis=1))
#tape.graidnet()를 이용하여 gradient계산
gradients=tape.gradient(loss,[w1,w2])

import tensorflow as tf
import numpy as np
N, D, H=64, 1000, 100

#tensorflow는 TF tensor를 사용하는데 이는 numpy array를 변환해서도 생성가능
x=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
y=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
w1=tf.Variable(tf.random.uniform((D,H)))
w2=tf.Variable(tf.random.uniform((H,D)))

learning_rate=1e-6
for t in range(50):
    with tf.GradientTape() as tape:
        #forward pass
        h=tf.maximum(tf.matmul(x,w1),0)
        y_pred=tf.matmul(h,w2)
        diff=y_pred-y
        loss=tf.reduce_mean(tf.reduce_sum(diff**2, axis=1))
    #tape.graidnet()를 이용하여 gradient계산
    gradients=tape.gradient(loss,[w1,w2])
    
    w1.assign(w1 - learning_rate * gradients[0])
    w2.assign(w2 - learning_rate * gradients[1])

2. TensorFlow : optimizer

import tensorflow as tf
import numpy as np
N, D, H=64, 1000, 100

x=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
y=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
w1=tf.Variable(tf.random.uniform((D,H)))
w2=tf.Variable(tf.random.uniform((H,D)))

optimizer=tf.optimizers.SGD(1e-6)

learning_rate=1e-6
for t in range(50):
    with tf.GradientTape() as tape:
        #forward pass
        h=tf.maximum(tf.matmul(x,w1),0)
        y_pred=tf.matmul(h,w2)
        diff=y_pred-y
        loss=tf.reduce_mean(tf.reduce_sum(diff**2, axis=1))
    gradients=tape.gradient(loss,[w1,w2])
    #optimizer
    optimizer.apply_gradients(zip(gradients,[w1,w2]))

3. TensorFlow : loss

import tensorflow as tf
import numpy as np
N, D, H=64, 1000, 100

x=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
y=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
w1=tf.Variable(tf.random.uniform((D,H)))
w2=tf.Variable(tf.random.uniform((H,D)))

optimizer=tf.optimizers.SGD(1e-6)

learning_rate=1e-6
for t in range(50):
    with tf.GradientTape() as tape:
        #forward pass
        h=tf.maximum(tf.matmul(x,w1),0)
        y_pred=tf.matmul(h,w2)
        diff=y_pred-y
        #loss
        loss=tf.losses.MeanSquaredError()(y_pred, y)
    gradients=tape.gradient(loss,[w1,w2])
    optimizer.apply_gradients(zip(gradients,[w1,w2]))

4. keras : high-level wrapper

import tensorflow as tf
import numpy as np
N, D, H=64, 1000, 100

x=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
y=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
model=tf.keras.Sequential()
model.add(tf.keras.layers.Dense(H, input_shape=(D,),
                                activation=tf.nn.relu))
model.add(tf.keras.layers.Dense(D))
optimizer=tf.optimizers.SGD(1e-1)

losses=[]
for t in range(50):
    with tf.GradientTape() as tape:
        #forward pass
        y_pred=model(x)
        loss=tf.losses.MeanSquaredError()(y_pred, y)
    gradients=tape.graident(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(gradients,model.trainable_variables))

import tensorflow as tf
import numpy as np
N, D, H=64, 1000, 100

x=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
y=tf.convert_to_tensor(np.random.randn(N,D),np.float32)
model=tf.keras.Sequential()
model.add(tf.keras.layers.Dense(H, input_shape=(D,),
                                activation=tf.nn.relu))
model.add(tf.keras.layers.Dense(D))
optimizer=tf.optimizers.SGD(1e-1)
model.compile(loss=tf.keras.losses.MeanSquaredError(),optimizer=optimizer)
history=model.fit(x,y,epochs=50, batch_size=N)

5. TensorFlow : Pretrained Models

tf.keras, TF-Slim

 

6. TensorFlow : Tensorboard

시각화 툴

 

7. TensorFlow : Distributed Version

그래프를 나눠서 각각의 머신에서 돌릴 수도 있음