[9주차 - Day2] Multilayer Perceptron

Deep Learning: 신경망의 기초 - 다층퍼셉트론

3. 다층 퍼셉트론

퍼셉트론은 선형 분류기(linear classifier)로 선형 분리 불가능한 상황에서 한계->다층 퍼셉트론의 등장

다층 퍼셉트론의 핵심 아이디어

• 은닉층(hidden layer)을 둠으로써 분류에 유리한 새로운 특징 공간으로 변환
• 시그모이드 활성함수 : 퍼셉트론은 계단함수를 활성함수로 사용하였음->경성(hard) 의사결정/다층 퍼셉트론은 연성(soft)의사결정이 가능한 시그모이드 함수를 활성함수로 사용, 출력이 연속값
• 오류 역전파 알고리즘을 사용함으로써 역방향으로 진행하면서 한 층씩 gradient를 계산하고 가중치를 갱신

3.1. 특징 공간 변환

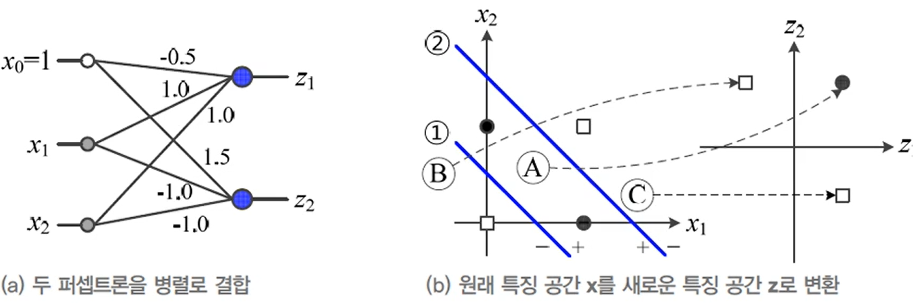
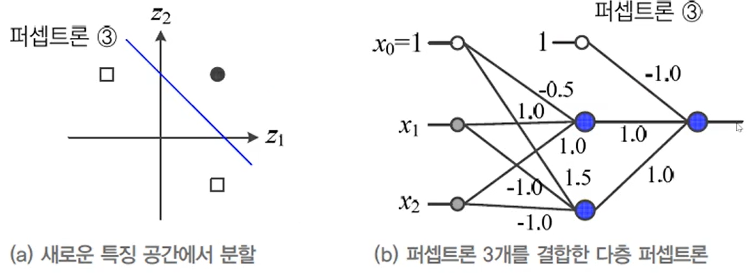
퍼셉트론을 병렬 결합하면 원래 공간을 새로운 특징 공간으로 변환->새로운 특징공간을 선형 분리하는 퍼셉트론을 순차 결합하면 다층 퍼셉트론

다층 퍼셉트론의 용량(capacity) : p개의 퍼셉트론을 결합하면 p차원 공간으로 변환

3.2. 활성함수

단일 퍼셉트론 : 계단 함수를 사용하여 영역을 점으로 변환=딱딱한 공간 분할

다층 퍼셉트론 : 그 외의 활성함수(로지스틱 시그모이드, 하이퍼볼릭 탄젠트 시그모이드, softplus, rectifier 등)를 사용하여 영역을 영역으로 변환=부드러운 공간 분할

신경망이 사용하는 다양한 활성함수

• 로지스틱 시그모이드와 하이퍼볼릭 탄젠트는 알파가 커질수록 계단 함수에 가까워짐
• 모두 1차 도함수 계산이 빠름
• 단일 퍼셉트론은 계단 함수
• 다층 퍼셉트론은 로지스틱 시그모이드와 하이퍼볼릭 탄젠트
• 심층학습은 ReLU(rectified linear activation)

시그모이드 함수(sigmoid fuction) : 대표적 비선형 함수, S자 모양의 함수를 활성함수로 사용

일반적으로 은닉층에서 로지스틱 시그모이드를 활성함수로 많이 사용

하지만 S자 모양의 넓은 포화곡선은 경사도 기반한 학습(오류 역전파)을 어렵게 하므로 깊은 신경망에서는 ReLU활용

3.3. 구조

d(특징의 개수)+1개의 입력->p개의 은닉층(p는 하이퍼 파라미터)->c(분류 개수)개의 출력

p가 너무 크면 과대적합, 너무 작으면 과소적합

U1:입력-은닉층 연결, 입력의 i번째 노드를 은닉층 j번째 노드와 연결U2:은닉층-출력 연결, 은닉층의 j번째 노드를 출력 k번째노드와 연결

범용적 근사 이론(universal approximation theorem) : 하나의 은닉층은 함수의 근사->다층 퍼셉트론도 공간을 변환하는 근사 함수

얕은 은닉층의 구조은 더 넓은 폭(width)이 필요할 수 있음=가중치가 더 많이 필요->과잉적합되기 쉬움->깊은(depth) 은닉층의 구조가 좋은 성능을 가짐 

은닉층의 깊이에 따른 이점

지수의 표현(exponential representation) : 각 은닉층은 입력 공간을 어디서 접을지(나눌지) 지정->지수적으로 많은 선형적인 영역 조각들이 생성 즉, 아무리 복잡하게 생긴 공간이래도 해결할 수 있음!->성능 향상

3.4. 동작

퍼셉트론을 특징 벡터 X를 출력벡터 O로 사상(mapping)하는 함수로 간주

깊은 신경망은 4개 이상일 때를 말함

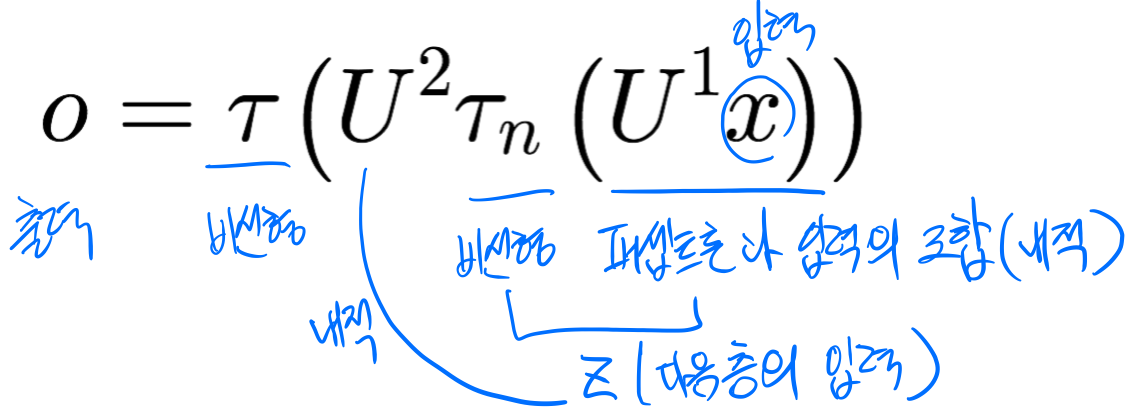
은닉층은 특징 추출기, 특징 벡터를 분류에 더 유리한 특징 공간으로 변환->특징학습(feature learning, data-driven features)

4. 오류 역전파 알고리즘

은닉층을 통한 특징공간의 변환

행렬 곱 : 회전 / 편향 : 이동 / 비선형 함수 : 왜곡

4.1. 목적함수의 정의 

훈련 집합 : 특징 벡터집합(X)과 부류 벡터집합(Y)

부류 벡터는 단발성(one-hot)코드로 표현

기계학습의 목표 : 모든 샘플을 옮게 분류하는 함수 f를 찾는 일

목적함수 : 평균 제곱 오차(mean squared error(MSE))로 정의

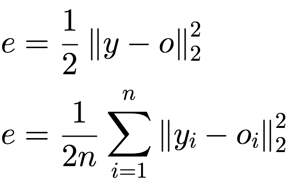
L2 norm을 이용한 온라인 모드(위)/배치모드(아래)

4.2. 오류 역전파 알고리즘의 설계

연산 그래프(computational graph)를 통해 나타냄

연쇄 법칙의 구현 : 반복되는 부분식들(subexpressions)을 저장하거나 재연산을 최소화

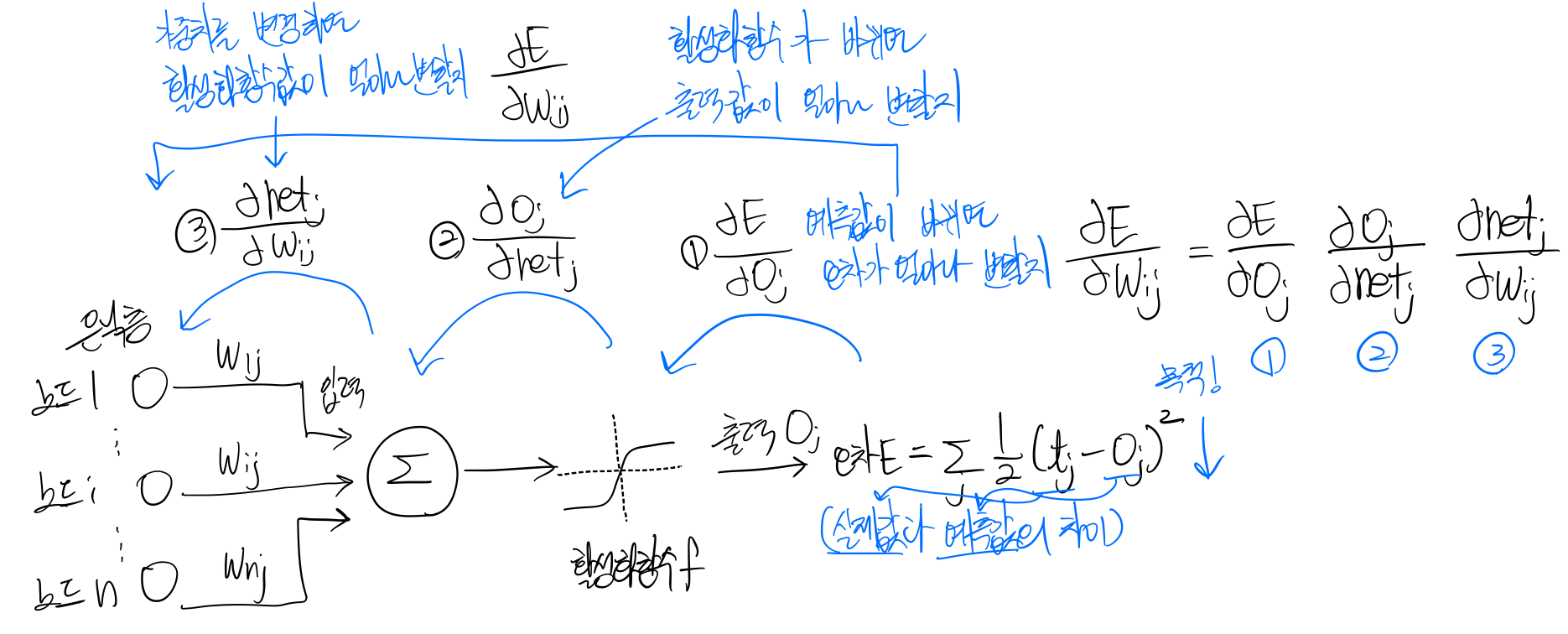
오류 역전파 알고리즘 : 출력의 오류를 역방향(왼쪽)으로 전파하며 경사도를 계산하는 알고리즘, 반복되는 부분식들의 경사도의 지수적 폭발(exponential explosion)이나 사라짐(vanishing)을 피해야함

역전파 분해(backprop with scalars) : downstran gradient=local gradient*upstram(=outstream) gradient

1. 단일 노드의 역전파 예

2. 곱셈의 역전파 예

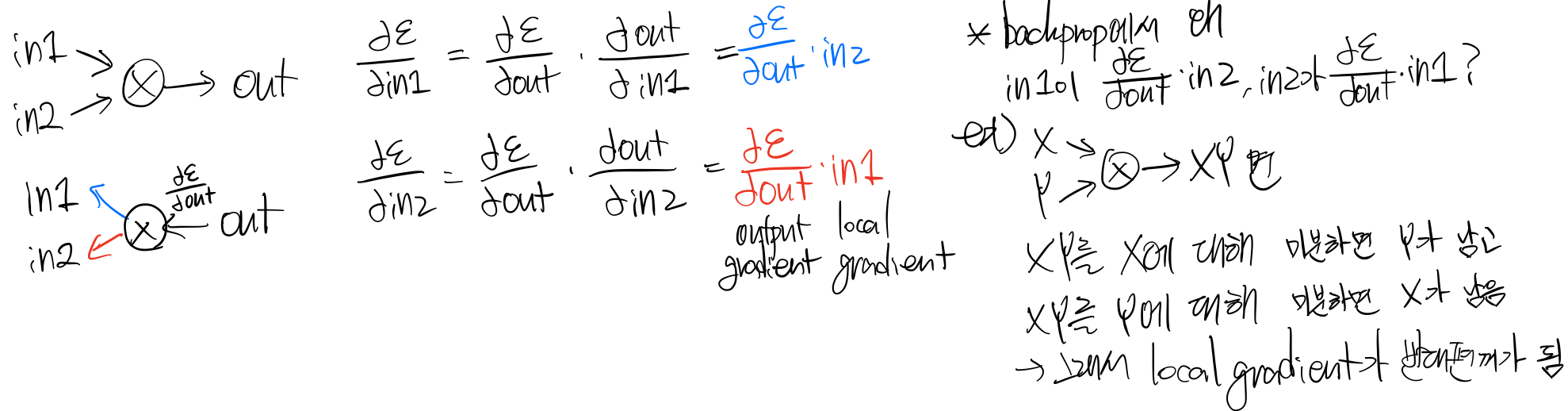
class Multiply(torch.autograd.Function):
	@staticmethod
	def forward(ctx, x, y):
    	ctx.save_for_backward(x,y)
        z=x*y
        return z
    @staticmethod
    def backward(ctx, grad_z):
    	x, y = ctx.saved_tensors
        grad_x = y * grad_z		#dz/dx*dL/dz
        grad_y = x * grad_z		#dz/dy*dL/dz
       	return grad_x, grad_y

3. 덧셈의 역전파 예

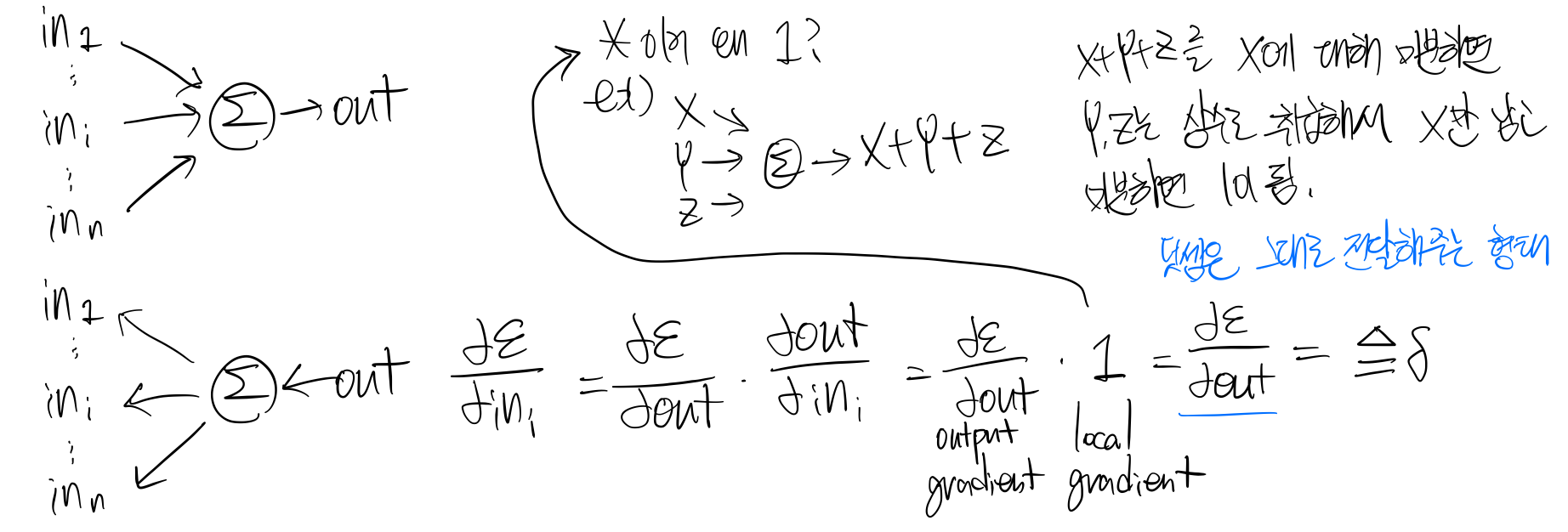
4. S자 모양 활성함수(시그모이드)의 역전파 예

5. 최대화(≒ReLU)의 역전파 예

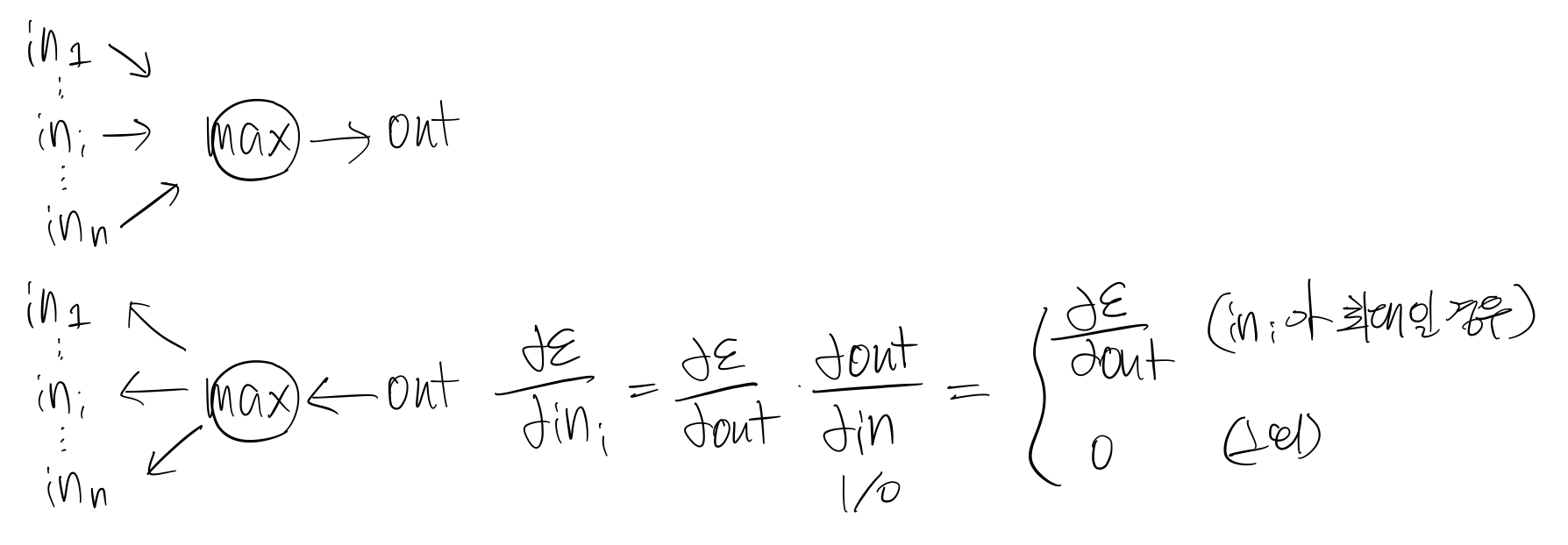
6. 전개(fanout)의 역전파 예

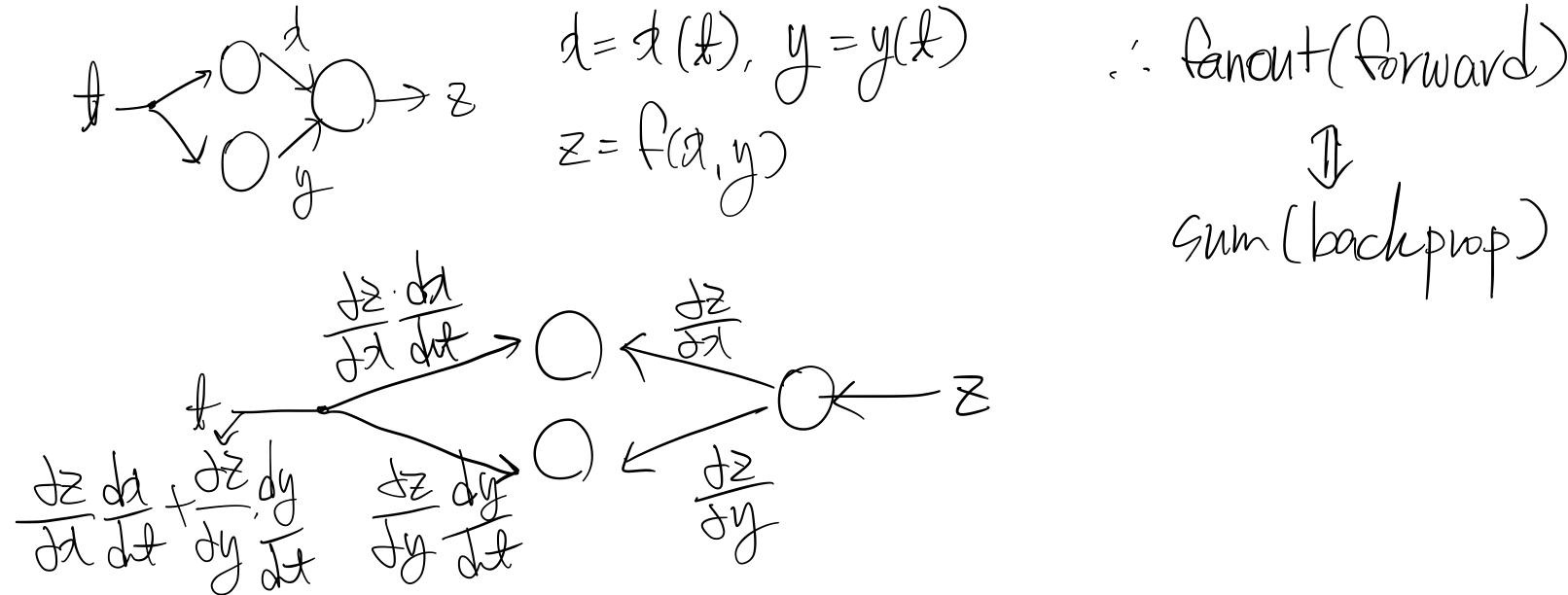
역전파의 주요 예

4.3. 오류 역전파를 이용한 학습 알고리즘

도함수의 종류

1. Scalar to Scalar : x를 변화시켰을 때 y가 어떻게 변하는지
2. Vector to Scalar(=Gradient) : 내가 관심있어하는 대상(y(출력값), scalar)은 1개고, 변화를 주는 값(x(입력값), vector)은 여러개 ex)Loss function
3. Vector to Vector(=Jacobian) : 내가 관심있어하는 대상(y(출력값), vector)이 여러개, 변화를 주는 값(x(입력값), vector)도 여러개

오류 역전파(error back-propagation)미분의 연쇄 법칙 이용

수 경우(scalar->scalar)미분

벡터인 경우

7. 다층 퍼셉트론의 특성

7.1. 오류 역전파 알고리즘의 빠른 속도

오류 역전파가 전방 계산 대비 1.5~2배의 시간 소요, 반복수행하기 때문

7.2. 모든 함수를 정확하게 근사할 수 있는 능력

은닉 노드가 충분히 많다면 활성 함수로 무엇을 사용하든 다층 퍼셉트론은 어떤 함수라도 근사화가능

7.3. 성능 향상을 위한 경험의 중요성

순수한 최적화 알고리즘으로는 높은 성능 불가능->데이터 희소성, 잡음, 미숙한 신경망 구조 등의 이유

신경망의 경험적 개발의 쟁점

• 아키텍처 : 은닉층과 은닉 노드의 개수
  • 은닉층과 은닉 노드를 늘리면 용량 증가, 추정해야할 매개변수 증가, 과잉적합 가능성 증가
• 초깃값 : 가중치 초기화
• 학습률 : 처음부터 끝까지 같은 학습률?or 큰 값에서 점점 줄이는 적응적 방식?
• 활성함수 : 초창기 다층 퍼셉트론은 로지스틱 시그모이드, tanh함수를 사용했으나 은닉층의 개수를 늘림에 따라 gradient vanishing같은 문제가 발생->ReLU함수 사용

Deep Learning: 신경망의 기초 - 실습III PT-TF 자동미분연산

PyTorch Tutorial - Autograd & MLP(Multi-layer perceptron)

나중에 참고하면 좋을 거 같은 블로그

https://teamdable.github.io/techblog/PyTorch-Autograd

PyTorch Autograd

Tensor

• torch.Tensor 클래스의 .requires_grad속성을 True로 설정하면 해당 텐서에서 이루어진 모든 연산 추적(track)
• 계산이 완료된 후 backward()를 호출하여 모든 변화도(gradient)를 자동으로 계산가능
• Tensor의 변화도(gradient)는 .grad 속성에 누적
• Tensor가 추적하는 걸 중단하려면 .detach()를 호출
• 기록을 추적하는 것을 방지하기 위해 with.torch.no_grad() : 로 코드를 감쌀 수 있는데 이는 변화도는(gradient)는 필요없지만 requires_grad=True가 설정되어 학습 가능한 매개변수를 갖는 모델을 평가(evaluate)할 때 유용
• Tensor와 Function은 서로 연결되어 있고 모든 연산과정을 부호화하여 순환하지 않는 그래프 생성
• 각 Tensor는 .grad_fn속성을 가지고 있는데 이는 Tensor를 생성한 Function을 참조
• 도함수를 계산하기 위해서는 Tensor의 .backward() 호출

import torch

# x의 연산 과적을 추적하기 위해 requires_grad=True로 설정
x = torch.ones(2, 2, requires_grad=True)
print(x)

# 직접 생선한 Tensor이기 때문에 grad_fn이 None인 것을 확인
#grad_fn속성 : Tensor를 생성한 Function 참조
print(x.grad_fn)
'''
tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
None
'''

# y, z, out은 연산의 결과로 생성된 것이기 때문에 grad_fn을 갖고 있는 것을 확인 가능
y = x + 2
z = y * y * 3
out = z.mean()

# 각각 사용한 func에 맞게 grad_fn이 생성된 것을 확인할 수 있음
print(y)
print(z)
print(out)
'''
tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward0>)
tensor([[27., 27.],
        [27., 27.]], grad_fn=<MulBackward0>)
tensor(27., grad_fn=<MeanBackward0>)
'''

#requires_grad값을 지정하지 않으면 기본 값은 False
a=torch.randn(2,2)
print(a.requires_grad)
#requires_grad_()를 사용하면 requires_grad값을 바꿀 수 있음
a.requires_grad_(True)
print(a.requires_grad)
'''
False
True
'''

#속성을 상속받음
b=(a*a).sum()
print(b)
print(b.requires_grad)
'''
tensor(1.5793, grad_fn=<SumBackward0>)
True
'''

 

변화도(gradient)

#이전에 만든 out을 사용해서 역전파 진행

#retain_grad() : leaf가 아닌 Tensor의 .grad속성 활성화
#중간값에 대한 미분값을 보고 싶다면 해당 값에 대한 retain_grad()호출해야함
y.retain_grad()
x.retain_grad()
z.retain_grad()
#backward() : 모든 변화도(gradient)를 자동으로 계산
#여러 번 미분을 진행하기 위해서는 retain_graph=True로 설정해줘야함(안 하면 에러)
out.backward(retain_graph=True)

print(x.grad)
print(y.grad)
print(z.grad)
'''
tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])
tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])
tensor([[0.2500, 0.2500],
        [0.2500, 0.2500]])
'''

x = torch.randn(3, requires_grad=True)
print(x)
y = x * 2
print(y)

#.data.norm() : L2 norm(Frobenius norm)
#=sqrt(sum(y의 모든 요소^2))
while y.data.norm() < 1000:
  y = y * 2

print(y)
'''
tensor([-0.3601, -1.3327,  0.3289], requires_grad=True)
tensor([-0.7203, -2.6655,  0.6578], grad_fn=<MulBackward0>)
tensor([ -368.7681, -1364.7264,   336.7958], grad_fn=<MulBackward0>)
'''

#with torch.no_grad()로 코드를 감싸서 autograd가 .requires_grad=True인 Tensor의 연산 기록을 추적하는 걸 멈추게 할 수 있음
print(x.requires_grad)
with torch.no_grad():
	print(x.requires_grad)
'''
True
False
'''

#또는 .detach()를 호출하여 내용물은 같지만 requires_grad가 다른 새로운 Tensor를 생성할 수도 있음
print(x.requires_grad)
y=x.detach()
print(y.requires_grad)
print(x.eq(y).all())
'''
True
Flase
tensor(True)	#내용물은 같음
'''

ANN(Artificial Neural Networks)

• 신경망은 torch.nn패키지를 사용하여 생성가능
• nn.Module은 layer와 output을 반환하는 forward(input)메소드 포함

예제)

• 간단한 순전파 네트워크(feed-forward-network)
• 입력을 받아 여러 계층(layer)에 차례로 전달 후 최종 출력 제공

신경망의 일반적인 학습 과정

1. 학습 가능한 매개변수(가중치)를 갖는 신경망 정의
2. 데이터 셋 입력 반복
3. 입력을 신경망에서 전파(process)
4. 손실(loss, 입력값-예측값)를 계산
5. 변화도(gradient)를 신경망의 매개변수들에 의해 역으로 전파(역전파)
6. 신경망의 가중치 갱신
   • 새로운 가중치=가중치-학습률*변화도

#라이브러리 import
import pandas as pd

from sklearn.datasets import load_iris

import torch
import torch.nn as nn
from torch.utils.data import DataLoader, TensorDataset

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()

        self.layer0 = nn.Linear(4, 128)
        self.layer1 = nn.Linear(128, 64)
        self.layer2 = nn.Linear(64, 32)
        self.layer3 = nn.Linear(32, 16)
        self.layer4 = nn.Linear(16, 3)

        self.bn0 = nn.BatchNorm1d(128)
        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(32)

        self.act = nn.ReLU()

    def forward(self, x):
      x = self.act(self.bn0(self.layer0(x)))
      x = self.act(self.bn1(self.layer1(x)))
      x = self.act(self.bn2(self.layer2(x)))
      x = self.act(self.layer3(x))
      x = self.layer4(x)

      return x

손실함수(Loss function)

• (output, target)을 한 쌍으로 입력받아 출력이 정답으로부터 얼마나 떨어져있는지 계산
• forward()만 정의하면 backward()는 autograd에 의해 자동 정의
• 모델의 학습 가능한 매개변수는 net.parameters()에 의해 변환

criterion = nn.CrossEntropyLoss()

ex_X, ex_y = torch.randn([4, 4]), torch.tensor([1, 0, 2, 0])
print('ex_X : ', ex_X)
print('ex_y : ', ex_y)

#모델 정의
net = Net()
#입력값을 모델로 훈련시킨 후 나온 출력값
output = net(ex_X)
print(output)
#손실계산
loss = criterion(output, ex_y)
#계산한 손실 출력
print('loss: ', loss.item())
  
net.zero_grad()

print('layer0.bias.grad before backward')
print(net.layer4.bias.grad)
print(net.layer4.bias.is_leaf)

loss.backward()

print('layer0.bias.grad after backward')
print(net.layer4.bias.grad)

'''
ex_X :  tensor([[-0.3045,  1.5439,  0.6195, -0.4642],
        [ 2.3502,  0.7011,  0.1095,  1.6037],
        [ 0.8238,  0.8151, -0.0307,  0.5803],
        [-0.6257,  0.8074, -0.0829,  0.3538]])
ex_y :  tensor([1, 0, 2, 0])
tensor([[ 0.4725, -0.5172,  0.0757],
        [ 0.2162, -0.0060,  0.1769],
        [ 0.1057, -0.1521,  0.0456],
        [ 0.2338, -0.3210,  0.1688]], grad_fn=<AddmmBackward>)
loss:  1.1750612258911133
layer0.bias.grad before backward
None
True
layer0.bias.grad after backward
tensor([-0.0955, -0.0037,  0.0993])
'''

#net.parameters()에는 각각의 층들마다의 weight, bias값들이 들어있음
#Linear Layer : 4, 128, 64, 32, 16, 3 -> 6개*2(wieght, bias) + BatchNorm1d Layer : 128, 64, 32->3개*2(weight, bias)
params = list(net.parameters())
for i in range(len(params)):
  print(params[i].size())
#print(params[0].size())   # layer0의 weight
'''
torch.Size([128, 4])
torch.Size([128])
torch.Size([64, 128])
torch.Size([64])
torch.Size([32, 64])
torch.Size([32])
torch.Size([16, 32])
torch.Size([16])
torch.Size([3, 16])
torch.Size([3])
torch.Size([128])
torch.Size([128])
torch.Size([64])
torch.Size([64])
torch.Size([32])
torch.Size([32])
'''

가중치 갱신

가장 단순한 갱신 규칙 : 확률적 경사 하강법(SGD, Stochastic Gradient Descent)

새로운 가중치 = 가중치 - 학습률 * 변화도

# torch.optim 패키지에 다양한 갱신 규칙이 규현되어 있음
import torch.optim as optim

optimizer = optim.SGD(net.parameters(), lr=0.001)

optimizer.zero_grad()
output = net(ex_X)
loss = criterion(output, ex_y)
loss.backward()
optimizer.step()  # 업데이트 진행

MLP 모델

#data load
dataset = load_iris()

data = dataset.data
label = dataset.target

print(dataset.DESCR)
'''
.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
                
    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988
'''

# 훈련과 테스트 데이터로 나누기
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(data, label, test_size=0.25)
print(len(X_train))
print(len(X_test))
'''
112
38
'''

# DataLoader 생성
# numpy->Tensor
X_train = torch.from_numpy(X_train).float()
y_train = torch.from_numpy(y_train).long()
X_test = torch.from_numpy(X_test).float()
y_test = torch.from_numpy(y_test).long()

train_set = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_set, batch_size=4, shuffle=True)

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()

        self.layer0 = nn.Linear(4, 128)
        self.layer1 = nn.Linear(128, 64)
        self.layer2 = nn.Linear(64, 32)
        self.layer3 = nn.Linear(32, 16)
        self.layer4 = nn.Linear(16, 3)

        self.bn0 = nn.BatchNorm1d(128)
        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(32)

        self.act = nn.ReLU()

    def forward(self, x):
      x = self.act(self.bn0(self.layer0(x)))
      x = self.act(self.bn1(self.layer1(x)))
      x = self.act(self.bn2(self.layer2(x)))
      x = self.act(self.layer3(x))
      x = self.layer4(x)

      return x
      # return nn.Softmax(x)

net = Net()
print(net)
'''
Net(
  (layer0): Linear(in_features=4, out_features=128, bias=True)
  (layer1): Linear(in_features=128, out_features=64, bias=True)
  (layer2): Linear(in_features=64, out_features=32, bias=True)
  (layer3): Linear(in_features=32, out_features=16, bias=True)
  (layer4): Linear(in_features=16, out_features=3, bias=True)
  (bn0): BatchNorm1d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (bn1): BatchNorm1d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (bn2): BatchNorm1d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (act): ReLU()
)
'''

optimizer = torch.optim.SGD(net.parameters(), lr=0.001)
criterion = nn.CrossEntropyLoss()
epochs = 200

losses = list()
accuracies = list()

for epoch in range(epochs):
  epoch_loss = 0  
  epoch_accuracy = 0
  for X, y in train_loader:
  
    optimizer.zero_grad()
    
    output = net(X)

    loss = criterion(output, y)
    loss.backward()
    
    optimizer.step()
    _, predicted = torch.max(output, dim=1)
    accuracy = (predicted == y).sum().item()
    epoch_loss += loss.item()
    epoch_accuracy += accuracy

  epoch_loss /= len(train_loader)
  epoch_accuracy /= len(X_train)
  print("epoch :{}, \tloss :{}, \taccuracy :{}".format(str(epoch+1).zfill(3),round(epoch_loss,4), round(epoch_accuracy,4)))
  
  losses.append(epoch_loss)
  accuracies.append(epoch_accuracy)
'''
epoch :001, 	loss :1.0802, 	accuracy :0.3929
epoch :002, 	loss :1.0772, 	accuracy :0.4107
epoch :003, 	loss :1.0432, 	accuracy :0.4911
epoch :004, 	loss :1.0192, 	accuracy :0.5268
epoch :005, 	loss :1.0083, 	accuracy :0.5446
epoch :006, 	loss :1.0125, 	accuracy :0.5089
epoch :007, 	loss :0.9974, 	accuracy :0.5446
epoch :008, 	loss :0.9648, 	accuracy :0.5714
epoch :009, 	loss :0.9501, 	accuracy :0.5893
epoch :010, 	loss :0.9663, 	accuracy :0.6071
epoch :011, 	loss :0.9263, 	accuracy :0.6518
epoch :012, 	loss :0.9243, 	accuracy :0.6607
epoch :013, 	loss :0.9241, 	accuracy :0.625
epoch :014, 	loss :0.9304, 	accuracy :0.6339
epoch :015, 	loss :0.9154, 	accuracy :0.6786
epoch :016, 	loss :0.8798, 	accuracy :0.7054
epoch :017, 	loss :0.8923, 	accuracy :0.7321
epoch :018, 	loss :0.9092, 	accuracy :0.7143
epoch :019, 	loss :0.9048, 	accuracy :0.7054
epoch :020, 	loss :0.8678, 	accuracy :0.7411
epoch :021, 	loss :0.8647, 	accuracy :0.7768
epoch :022, 	loss :0.8266, 	accuracy :0.7768
epoch :023, 	loss :0.8726, 	accuracy :0.7054
epoch :024, 	loss :0.8343, 	accuracy :0.7946
epoch :025, 	loss :0.8072, 	accuracy :0.7589
epoch :026, 	loss :0.8605, 	accuracy :0.7054
epoch :027, 	loss :0.7897, 	accuracy :0.8036
epoch :028, 	loss :0.8635, 	accuracy :0.7321
epoch :029, 	loss :0.7856, 	accuracy :0.8125
epoch :030, 	loss :0.7993, 	accuracy :0.7946
epoch :031, 	loss :0.7767, 	accuracy :0.7679
epoch :032, 	loss :0.7829, 	accuracy :0.7232
epoch :033, 	loss :0.7437, 	accuracy :0.8304
epoch :034, 	loss :0.7574, 	accuracy :0.7679
epoch :035, 	loss :0.7197, 	accuracy :0.7768
epoch :036, 	loss :0.7798, 	accuracy :0.7589
epoch :037, 	loss :0.8109, 	accuracy :0.7054
epoch :038, 	loss :0.7733, 	accuracy :0.7679
epoch :039, 	loss :0.7605, 	accuracy :0.7589
epoch :040, 	loss :0.7155, 	accuracy :0.8036
epoch :041, 	loss :0.7275, 	accuracy :0.7321
epoch :042, 	loss :0.6755, 	accuracy :0.8214
epoch :043, 	loss :0.7323, 	accuracy :0.7768
epoch :044, 	loss :0.7076, 	accuracy :0.8036
epoch :045, 	loss :0.6614, 	accuracy :0.8214
epoch :046, 	loss :0.6984, 	accuracy :0.7768
epoch :047, 	loss :0.7199, 	accuracy :0.75
epoch :048, 	loss :0.6872, 	accuracy :0.8036
epoch :049, 	loss :0.6426, 	accuracy :0.8214
epoch :050, 	loss :0.64, 	accuracy :0.8393
epoch :051, 	loss :0.6557, 	accuracy :0.8125
epoch :052, 	loss :0.604, 	accuracy :0.8393
epoch :053, 	loss :0.6885, 	accuracy :0.7857
epoch :054, 	loss :0.7239, 	accuracy :0.7589
epoch :055, 	loss :0.7267, 	accuracy :0.7321
epoch :056, 	loss :0.6695, 	accuracy :0.7768
epoch :057, 	loss :0.5948, 	accuracy :0.8393
epoch :058, 	loss :0.7046, 	accuracy :0.7679
epoch :059, 	loss :0.6853, 	accuracy :0.75
epoch :060, 	loss :0.6209, 	accuracy :0.8125
epoch :061, 	loss :0.5772, 	accuracy :0.8214
epoch :062, 	loss :0.645, 	accuracy :0.7857
epoch :063, 	loss :0.665, 	accuracy :0.7679
epoch :064, 	loss :0.7714, 	accuracy :0.6429
epoch :065, 	loss :0.5995, 	accuracy :0.8125
epoch :066, 	loss :0.624, 	accuracy :0.8036
epoch :067, 	loss :0.5548, 	accuracy :0.8393
epoch :068, 	loss :0.6048, 	accuracy :0.7946
epoch :069, 	loss :0.665, 	accuracy :0.7589
epoch :070, 	loss :0.5627, 	accuracy :0.8125
epoch :071, 	loss :0.6663, 	accuracy :0.7589
epoch :072, 	loss :0.6872, 	accuracy :0.7054
epoch :073, 	loss :0.5294, 	accuracy :0.8839
epoch :074, 	loss :0.6545, 	accuracy :0.7679
epoch :075, 	loss :0.5874, 	accuracy :0.7679
epoch :076, 	loss :0.5968, 	accuracy :0.7679
epoch :077, 	loss :0.6385, 	accuracy :0.7232
epoch :078, 	loss :0.6169, 	accuracy :0.7679
epoch :079, 	loss :0.5014, 	accuracy :0.8393
epoch :080, 	loss :0.5602, 	accuracy :0.8214
epoch :081, 	loss :0.6103, 	accuracy :0.7679
epoch :082, 	loss :0.5439, 	accuracy :0.8214
epoch :083, 	loss :0.4735, 	accuracy :0.8571
epoch :084, 	loss :0.5493, 	accuracy :0.8125
epoch :085, 	loss :0.6318, 	accuracy :0.7589
epoch :086, 	loss :0.492, 	accuracy :0.8571
epoch :087, 	loss :0.5707, 	accuracy :0.7679
epoch :088, 	loss :0.6774, 	accuracy :0.6964
epoch :089, 	loss :0.6354, 	accuracy :0.7321
epoch :090, 	loss :0.4971, 	accuracy :0.8393
epoch :091, 	loss :0.5397, 	accuracy :0.8036
epoch :092, 	loss :0.5211, 	accuracy :0.8304
epoch :093, 	loss :0.541, 	accuracy :0.7946
epoch :094, 	loss :0.5316, 	accuracy :0.8304
epoch :095, 	loss :0.5374, 	accuracy :0.7946
epoch :096, 	loss :0.4877, 	accuracy :0.8571
epoch :097, 	loss :0.463, 	accuracy :0.8661
epoch :098, 	loss :0.524, 	accuracy :0.7946
epoch :099, 	loss :0.7406, 	accuracy :0.6607
epoch :100, 	loss :0.5324, 	accuracy :0.7589
epoch :101, 	loss :0.4757, 	accuracy :0.8125
epoch :102, 	loss :0.4898, 	accuracy :0.8125
epoch :103, 	loss :0.6157, 	accuracy :0.7768
epoch :104, 	loss :0.5665, 	accuracy :0.7589
epoch :105, 	loss :0.5077, 	accuracy :0.8482
epoch :106, 	loss :0.5496, 	accuracy :0.7768
epoch :107, 	loss :0.5045, 	accuracy :0.8214
epoch :108, 	loss :0.5308, 	accuracy :0.7857
epoch :109, 	loss :0.4637, 	accuracy :0.8482
epoch :110, 	loss :0.4986, 	accuracy :0.8036
epoch :111, 	loss :0.531, 	accuracy :0.7679
epoch :112, 	loss :0.4691, 	accuracy :0.8304
epoch :113, 	loss :0.4971, 	accuracy :0.8036
epoch :114, 	loss :0.4626, 	accuracy :0.8393
epoch :115, 	loss :0.5284, 	accuracy :0.7946
epoch :116, 	loss :0.4612, 	accuracy :0.8125
epoch :117, 	loss :0.4205, 	accuracy :0.8661
epoch :118, 	loss :0.5266, 	accuracy :0.7768
epoch :119, 	loss :0.4128, 	accuracy :0.875
epoch :120, 	loss :0.4115, 	accuracy :0.8839
epoch :121, 	loss :0.536, 	accuracy :0.7857
epoch :122, 	loss :0.5868, 	accuracy :0.7768
epoch :123, 	loss :0.5373, 	accuracy :0.7679
epoch :124, 	loss :0.4723, 	accuracy :0.8393
epoch :125, 	loss :0.5095, 	accuracy :0.8214
epoch :126, 	loss :0.4307, 	accuracy :0.8393
epoch :127, 	loss :0.4439, 	accuracy :0.8304
epoch :128, 	loss :0.5364, 	accuracy :0.7679
epoch :129, 	loss :0.4876, 	accuracy :0.8036
epoch :130, 	loss :0.5586, 	accuracy :0.8125
epoch :131, 	loss :0.507, 	accuracy :0.7768
epoch :132, 	loss :0.4527, 	accuracy :0.8661
epoch :133, 	loss :0.5104, 	accuracy :0.7946
epoch :134, 	loss :0.5751, 	accuracy :0.7321
epoch :135, 	loss :0.5047, 	accuracy :0.8036
epoch :136, 	loss :0.4892, 	accuracy :0.8304
epoch :137, 	loss :0.4954, 	accuracy :0.7946
epoch :138, 	loss :0.4744, 	accuracy :0.8125
epoch :139, 	loss :0.4746, 	accuracy :0.8214
epoch :140, 	loss :0.5161, 	accuracy :0.7857
epoch :141, 	loss :0.4012, 	accuracy :0.8571
epoch :142, 	loss :0.492, 	accuracy :0.7411
epoch :143, 	loss :0.4188, 	accuracy :0.8482
epoch :144, 	loss :0.4566, 	accuracy :0.8393
epoch :145, 	loss :0.4629, 	accuracy :0.8214
epoch :146, 	loss :0.4248, 	accuracy :0.8393
epoch :147, 	loss :0.4184, 	accuracy :0.8571
epoch :148, 	loss :0.4564, 	accuracy :0.8214
epoch :149, 	loss :0.3769, 	accuracy :0.875
epoch :150, 	loss :0.4183, 	accuracy :0.8304
epoch :151, 	loss :0.4302, 	accuracy :0.8929
epoch :152, 	loss :0.5295, 	accuracy :0.7411
epoch :153, 	loss :0.4457, 	accuracy :0.8036
epoch :154, 	loss :0.4223, 	accuracy :0.8036
epoch :155, 	loss :0.4397, 	accuracy :0.8125
epoch :156, 	loss :0.5142, 	accuracy :0.75
epoch :157, 	loss :0.3626, 	accuracy :0.875
epoch :158, 	loss :0.3966, 	accuracy :0.8839
epoch :159, 	loss :0.449, 	accuracy :0.8036
epoch :160, 	loss :0.4681, 	accuracy :0.8036
epoch :161, 	loss :0.4476, 	accuracy :0.8125
epoch :162, 	loss :0.3629, 	accuracy :0.8839
epoch :163, 	loss :0.4295, 	accuracy :0.8214
epoch :164, 	loss :0.4731, 	accuracy :0.8125
epoch :165, 	loss :0.4013, 	accuracy :0.8393
epoch :166, 	loss :0.4912, 	accuracy :0.8125
epoch :167, 	loss :0.4242, 	accuracy :0.8393
epoch :168, 	loss :0.4508, 	accuracy :0.7946
epoch :169, 	loss :0.3011, 	accuracy :0.9286
epoch :170, 	loss :0.3608, 	accuracy :0.8571
epoch :171, 	loss :0.4456, 	accuracy :0.7946
epoch :172, 	loss :0.3947, 	accuracy :0.8661
epoch :173, 	loss :0.4095, 	accuracy :0.8125
epoch :174, 	loss :0.4935, 	accuracy :0.7857
epoch :175, 	loss :0.4462, 	accuracy :0.8393
epoch :176, 	loss :0.3973, 	accuracy :0.8214
epoch :177, 	loss :0.4276, 	accuracy :0.8304
epoch :178, 	loss :0.3451, 	accuracy :0.8661
epoch :179, 	loss :0.3684, 	accuracy :0.8482
epoch :180, 	loss :0.4851, 	accuracy :0.7768
epoch :181, 	loss :0.3692, 	accuracy :0.875
epoch :182, 	loss :0.4498, 	accuracy :0.8036
epoch :183, 	loss :0.3647, 	accuracy :0.875
epoch :184, 	loss :0.4833, 	accuracy :0.8214
epoch :185, 	loss :0.3794, 	accuracy :0.875
epoch :186, 	loss :0.4417, 	accuracy :0.8214
epoch :187, 	loss :0.3532, 	accuracy :0.8571
epoch :188, 	loss :0.3819, 	accuracy :0.875
epoch :189, 	loss :0.3959, 	accuracy :0.8571
epoch :190, 	loss :0.4093, 	accuracy :0.8036
epoch :191, 	loss :0.3643, 	accuracy :0.8482
epoch :192, 	loss :0.457, 	accuracy :0.7946
epoch :193, 	loss :0.417, 	accuracy :0.8482
epoch :194, 	loss :0.5968, 	accuracy :0.7589
epoch :195, 	loss :0.4521, 	accuracy :0.7857
epoch :196, 	loss :0.3347, 	accuracy :0.875
epoch :197, 	loss :0.5122, 	accuracy :0.7589
epoch :198, 	loss :0.4097, 	accuracy :0.8393
epoch :199, 	loss :0.4337, 	accuracy :0.8214
epoch :200, 	loss :0.3668, 	accuracy :0.8839
'''

# Plot result

import matplotlib.pyplot as plt

plt.figure(figsize=(20,5))
plt.subplots_adjust(wspace=0.2)

plt.subplot(1,2,1)
plt.title("$loss$",fontsize = 18)
plt.plot(losses)
plt.grid()
plt.xlabel("$epochs$", fontsize = 16)
plt.xticks(fontsize = 14)
plt.yticks(fontsize = 14)


plt.subplot(1,2,2)
plt.title("$accuracy$", fontsize = 18)
plt.plot(accuracies)
plt.grid()
plt.xlabel("$epochs$", fontsize = 16)
plt.xticks(fontsize = 14)
plt.yticks(fontsize = 14)

plt.show()

# Test

output = net(X_test)
print(torch.max(output, dim=1))
_, predicted = torch.max(output, dim=1)
accuracy = round((predicted == y_test).sum().item() / len(y_test),4)

print("test_set accuracy :", round(accuracy,4))
'''
torch.return_types.max(
values=tensor([1.7726, 2.2291, 0.9847, 0.4993, 0.9977, 1.4347, 0.7652, 1.7363, 1.2362,
        3.1726, 0.5636, 1.6254, 0.5907, 0.6640, 1.1971, 3.4562, 1.4861, 3.1303,
        0.9910, 2.2049, 1.7313, 1.9316, 0.8684, 0.9353, 1.2167, 0.5826, 1.9199,
        1.1493, 3.3740, 1.4999, 3.2217, 1.7139, 1.4012, 2.9030, 1.9455, 3.4471,
        0.8879, 3.3147], grad_fn=<MaxBackward0>),
indices=tensor([2, 2, 1, 1, 2, 1, 2, 1, 1, 0, 2, 2, 2, 2, 1, 0, 1, 0, 2, 1, 1, 0, 1, 2,
        2, 2, 2, 2, 0, 1, 0, 1, 2, 0, 1, 0, 1, 0]))
test_set accuracy : 0.9737
'''

Tensorflow-Tutorial(GradientTape, MLP)

그래디언트 테이프

• 자동미분을 위한 tf.GradientTape API제공
• tf.GradientTape는 모든 연산을 테이프에 기록
• 후진 방식 자동 미분(reverse mode differetiation)을 사용해서 테이프에 기록된 연산 그래디언트 계산

import tensorflow as tf

x = tf.ones((2, 2))
# 1, 1
# 1, 1
with tf.GradientTape() as t:
  t.watch(x)
  #reduce_sum() : 특정 축을 기준으로 합을 구해줌, 아무것도 입력 안 하면 모든 요소의 합
  y = tf.reduce_sum(x)
  print('y: ', y)
  z = tf.multiply(y, y)
  print('z: ', z)

# 입력 텐서 x에 대한 z의 도함수
#
dz_dx = t.gradient(z, x)
print(dz_dx)

for i in [0, 1]:
  for j in [0, 1]:
    # dz_dx[i][j]가 8이 아니면 AssertionError
    assert dz_dx[i][j].numpy() == 8.0
'''
y:  tf.Tensor(4.0, shape=(), dtype=float32)
z:  tf.Tensor(16.0, shape=(), dtype=float32)
tf.Tensor(
[[8. 8.]
 [8. 8.]], shape=(2, 2), dtype=float32)
 #z=4^2라서 8
'''

#GradientTape.gradient() 메소드가 호출되면 GradientTape에 포함된 리소스가 해제
#동일한 연산에 대해 여러 gradient를 계산하려면 지속성있는(persistent=True) 그래디언트 테이프 생성하면됨
#이렇게 생성한 그래디언트 테이프는 gradient()메소드의 다중 호출 허용
x = tf.constant(3.0)
print(x)
with tf.GradientTape(persistent=True) as t:
  t.watch(x)
  y = x * x
  z = y * y.  # z = x ^ 4
dz_dx = t.gradient(z, x)  # 108.0 (4*x^3 at x = 3)
print(dz_dx)
dy_dx = t.gradient(y, x)  # 6.0   (2 * x at x = 3)
print(dy_dx)
del t  # 테이프에 대한 참조를 삭제합니다.
'''
tf.Tensor(3.0, shape=(), dtype=float32)
tf.Tensor(108.0, shape=(), dtype=float32)
tf.Tensor(6.0, shape=(), dtype=float32)
'''

제어 흐름 기록

def f(x, y):
  output = 1.0
  for i in range(y):
    if i > 1 and i < 5:   #i가 2,3,4일 때 output*=x output은 x^n승
      output = tf.multiply(output, x)
  return output

def grad(x, y):
  with tf.GradientTape() as t:
    t.watch(x)
    out = f(x, y)
  return t.gradient(out, x)

x = tf.convert_to_tensor(2.0)
print(x)

print(grad(x, 6).numpy())	#output=2^3->gradient=3*2^2
assert grad(x, 6).numpy() == 12.0

print(grad(x, 5).numpy())	#output=2^3->gradient=3*2^2
assert grad(x, 5).numpy() == 12.0

print(grad(x, 4).numpy()) 	#output=2^2->gradient=2*2^1
assert grad(x, 4).numpy() == 4.0
'''
tf.Tensor(2.0, shape=(), dtype=float32)
12.0
12.0
4.0
'''

고계도(Higher-order) 그래디언트

x = tf.Variable(1.0) 
print(x)

with tf.GradientTape() as t:
  with tf.GradientTape() as t2:
    y = x * x * x
  dy_dx = t2.gradient(y, x)      # dy_dx = 3 * x^2 at x = 1
d2y_dx2 = t.gradient(dy_dx, x)   # d2y_dx2 = 6 * x at x = 1

assert dy_dx.numpy() == 3.0
assert d2y_dx2.numpy() == 6.0
print(dy_dx)
print(d2y_dx2)
'''
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=1.0>
tf.Tensor(3.0, shape=(), dtype=float32)
tf.Tensor(6.0, shape=(), dtype=float32)
'''

ANN(Artificial Neural Network)

Sequential 모델을 사용하는 경우

Seuquential 모델은 각 레이어에 정확히 하나의 입력 Tensor와 하나의 출력 Tensor가 있는 일반 레이어 스택에 적합

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

# Define Sequential model with 3 layers
model = keras.Sequential(
    [
        layers.Dense(2, activation="relu", name="layer1"),  # Pytorch - nn.Linear 
        layers.Dense(3, activation="relu", name="layer2"),
        layers.Dense(4, name="layer3"),
    ]
)
'''
# add() 메서드를 통해서 Sequential 모델을 점진적으로 작성할 수도 있음
model = keras.Sequential()
model.add(layers.Dense(2, activation="relu"))
model.add(layers.Dense(3, activation="relu"))
model.add(layers.Dense(4))
'''
# Call model on a test input
x = tf.ones((3, 3))
# [1, 1, 1] --> [o, o] --> [o, o, o] --> [o, o, o, o]
y = model(x)
print(y)
'''

tf.Tensor(
[[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]], shape=(3, 4), dtype=float32)
 '''

패션 MNIST를 사용한 분류 문제

10개의 카테고리, 70000개의 흑백이미지(28*28)

훈련에 60000개, 평가에 10000개 사용

# tensorflow와 tf.keras를 임포트합니다
import tensorflow as tf
from tensorflow import keras

# 헬퍼(helper) 라이브러리를 임포트합니다
import numpy as np
import matplotlib.pyplot as plt

fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()

class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
               'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']

데이터 전처리

# 신경망 모델에 주입하기 전에 값의 범위를 0~1로 조정
train_images = train_images / 255.0
test_images = test_images / 255.0

모델구성

model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(10, activation='softmax')
])
model.summary()
'''
Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
flatten (Flatten)            (None, 784)               0         
_________________________________________________________________
dense (Dense)                (None, 128)               100480    
_________________________________________________________________
dense_1 (Dense)              (None, 10)                1290      
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
'''

keras.utils.plot_model(model, show_shapes=True)

model.compile(optimizer='adam', # SGD, SGD + momentum
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5)
'''
Epoch 1/5
1875/1875 [==============================] - 5s 2ms/step - loss: 0.6372 - accuracy: 0.7811
Epoch 2/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.3899 - accuracy: 0.8604
Epoch 3/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.3421 - accuracy: 0.8763
Epoch 4/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.3163 - accuracy: 0.8843
Epoch 5/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.2913 - accuracy: 0.8917
<tensorflow.python.keras.callbacks.History at 0x7fae3b3971d0>
'''

test_loss, test_acc = model.evaluate(test_images,  test_labels, verbose=2)

print("Test loss:", test_loss)
print("Test accuracy:", test_acc)
'''
313/313 - 0s - loss: 0.3790 - accuracy: 0.8665
Test loss: 0.37901976704597473
Test accuracy: 0.8665000200271606
'''

# 훈련된 모델을 사용하여 이미지에 대한 예측 만들기
predictions = model.predict(test_images)
# 테스트 세트에 있는 각 이미지에 대한 예측을 진행한 후, 첫번째 예측 값
# 10개의 옷 품목에 상응하는 모델의 신뢰도(confidence)를 나타냄
predictions[0]
'''
array([2.3028070e-07, 3.7710961e-08, 1.5030743e-08, 7.9795255e-09,
       4.3214703e-09, 1.9712974e-03, 3.0058422e-07, 6.4831404e-03,
       1.1724497e-05, 9.9153322e-01], dtype=float32)
'''

# 가장 높은 신뢰도를 가진 레이블 출력
print(np.argmax(predictions[0]))
# 실제 테스트 데이터의 0번째 값
print(test_labels[0])
'''
9
9
'''

# 10개의 클래스에 대한 예측을 모두 그래프로 표현
# 올바르게 예측된 레이블은 파란색으로, 잘못 예측된 레이블은 빨강색으로 표현
# 숫자는 예측 레이블의 신뢰도 퍼센트
def plot_image(i, predictions_array, true_label, img):
  predictions_array, true_label, img = predictions_array[i], true_label[i], img[i]
  plt.grid(False)
  plt.xticks([])
  plt.yticks([])

  plt.imshow(img, cmap=plt.cm.binary)

  predicted_label = np.argmax(predictions_array)
  if predicted_label == true_label:
    color = 'blue'
  else:
    color = 'red'

  plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
                                100*np.max(predictions_array),
                                class_names[true_label]),
                                color=color)

def plot_value_array(i, predictions_array, true_label):
  predictions_array, true_label = predictions_array[i], true_label[i]
  plt.grid(False)
  plt.xticks([])
  plt.yticks([])
  thisplot = plt.bar(range(10), predictions_array, color="#777777")
  plt.ylim([0, 1])
  predicted_label = np.argmax(predictions_array)

  thisplot[predicted_label].set_color('red')
  thisplot[true_label].set_color('blue')

# 처음 X 개의 테스트 이미지와 예측 레이블, 진짜 레이블을 출력합니다
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
  plt.subplot(num_rows, 2*num_cols, 2*i+1)
  plot_image(i, predictions, test_labels, test_images)
  plt.subplot(num_rows, 2*num_cols, 2*i+2)
  plot_value_array(i, predictions, test_labels)
plt.show()