[6주차 - Day2] ML_basics - Decision Theory & Linear Regression

1. Machine Learning 기초 - 결정이론

결정이론이란?

새로운 값 x가 주어졌을 때 확률모델 p(x,t)에 기반해 최적의 결정을 내리는 것

추론단계 : 결합확률분포 p(x, Ck)를 구하는 것

결정단계 : 상황에 대한 확률이 주어졌을 때 어떻게 최적의 결정을 내릴 것인지?

p(ck|x)를 최대화시키는 k를 구하는 것이 좋은 결정

결정이론 - 이진분류(Binary Classification)

결정영역(decision region)

x가 Ci클래스로 분류를 하게 되면 x는 Ri에 속하게 된다

각각의 Ri는 클래스i에 속하는 모든 x의 집합

분류오류 확률(probability of misclassfication)

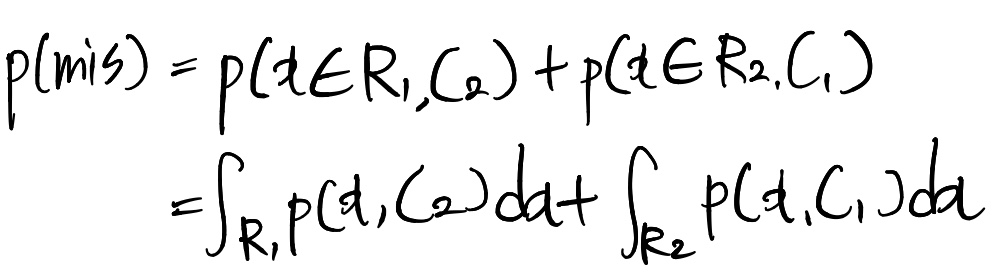
위 그림으로 봤을때 전체 오류의 종류는 2가지 :

x가 C2에 있는데 C1으로 잘못 분류+x가 C1에 있는데 C2로 잘못 분류

=>초록색+빨간색영역+파란색 영역

->이 영역은 hat(x)의 위치에 따라 달라질 것

오류를 최소화하려면 hat(x)를 x0까지 옮기면 됨

결정이론 - Multiclass일 경우

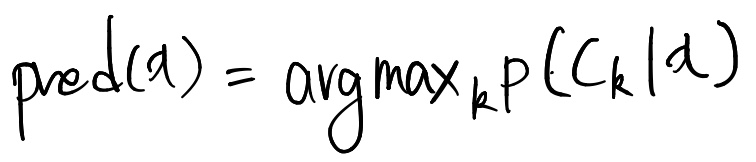
결정이론의 목표(분류의 경우)

결합확률분포 p(x, Ck)가 주어졌을때 최적의 결정영역들(R1, ..., Rk)를 찾는 것

기대손실 최소화(Minimizing the Expected Loss)

모든 결정이 동일한 리스크를 갖는 것은 아님 ex)암이 아닌데 맞는 것으로 진단<암이 맞는데 아닌 것으로 진단

손실행렬(loss matrix)

Lkj(k번째행 j번째열에 있는 원소의 값의 의미)

: Ck에 속하는 x를 Cj로 분류할 때 발생하는 손실(또는 비용)

행 : 실제 클래스

열 : 어떻게 분류했는지

 

기대손실

손실의 기댓값을 최소화하는 것이 목표

범함수를 최소화시키는 함수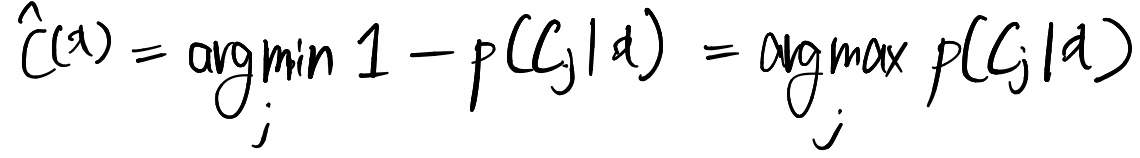

손실행렬이 0-1 loss인 경우(주대각선 원소 : 0 나머지 : 1)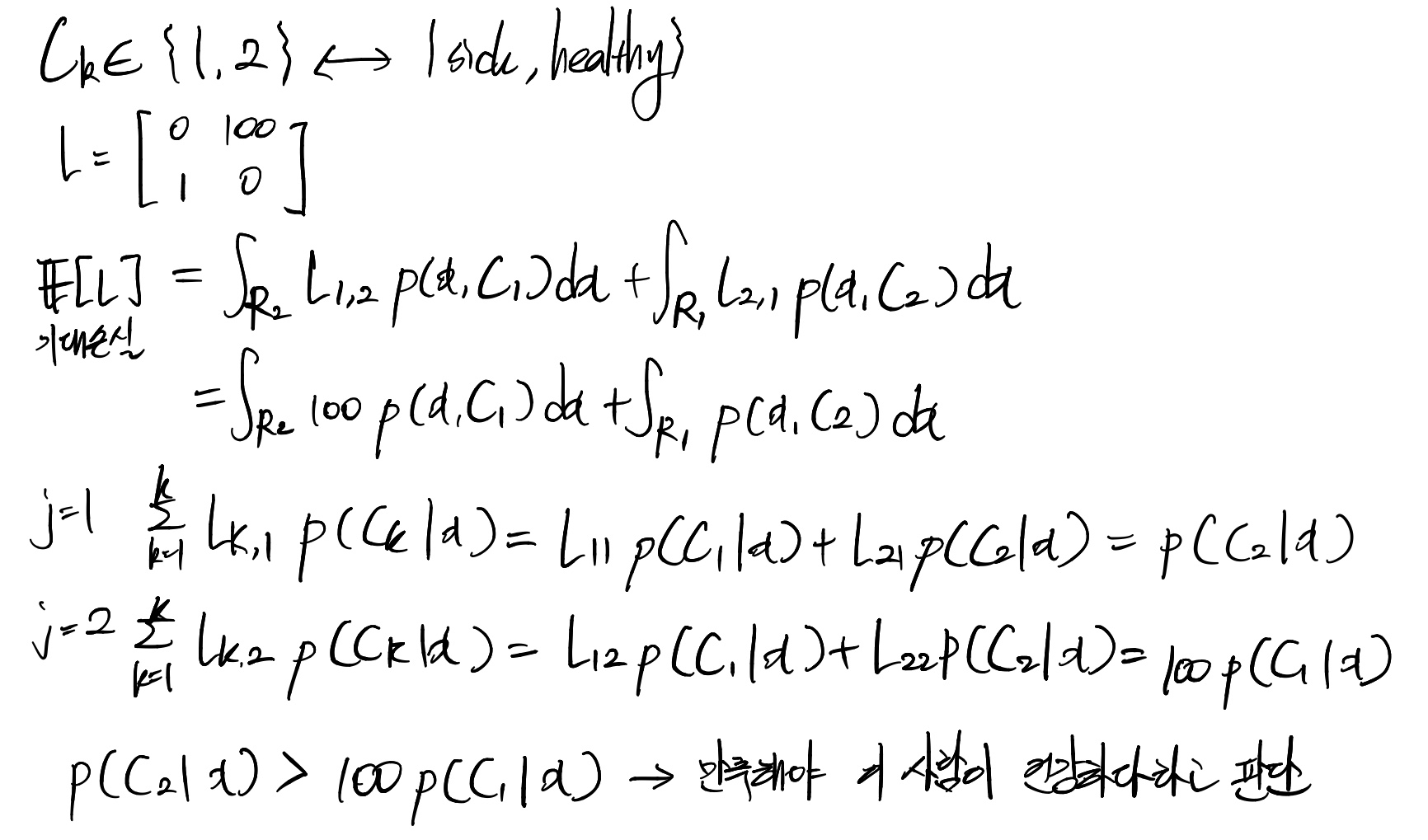

예제

결정이론 - 회귀문제의 경우

목표값 : t

손실함수 : L(t, y(x))={y(x)-t}^2

손실함수의 기대값

^p^??

 

2. Machine Learning 기초 - 선형회귀

1 .데이터가 선형적인 관계일 경우

2. 데이터가 비선형적인 관계일 경우

비선형데이터를 선형함수로 모델링하는 한가지 방법 : 기저함수(basis function)을 사용

최종모델은 여전히 계수(a)에 관해서 선형함수

다항기저함수(Polynomial Basis Functions)

Scikit-Learn은 PolynomialFeatures라는 transformer를 이미 포함

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import numpy as np

from sklearn.preprocessing import PolynomialFeatures
x=np.array([2,3,4])   
poly=PolynomialFeatures(3, include_bias=False)  #3차수까지 확장
poly.fit_transform(x[:,None])
'''
array([[ 2.,  4.,  8.],
       [ 3.,  9., 27.],
       [ 4., 16., 64.]])
'''

#7차원 변환
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
poly_model=make_pipeline(PolynomialFeatures(7),LinearRegression())

rng=np.random.RandomState(1)
x=10*rng.rand(50)   #(0~1)*10 난수 50개
y=np.sin(x)+0.1*rng.randn(50) 
plt.scatter(x,y)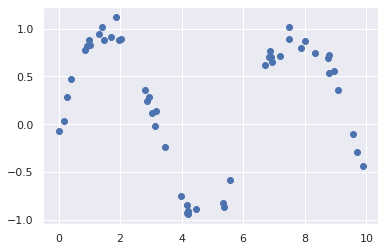

poly_model.fit(x[:,np.newaxis],y)   #데이터 변환+결과에 대해 선형회귀
#x[:, np.newaxis]->한 차원 확장 y->타겟값
xfit=np.linspace(0,10,1000) 
#linearly spaced linspace(start, stop, num)
#0이 배열의 시작값, 10이 배열의 끝값, 0과 10사이 1000개의 간격으로 요소
yfit=poly_model.predict(xfit[:,np.newaxis]) #x값들에 대해 예측값들이 어떤 것인지 저장

plt.scatter(x,y)
plt.plot(xfit, yfit);

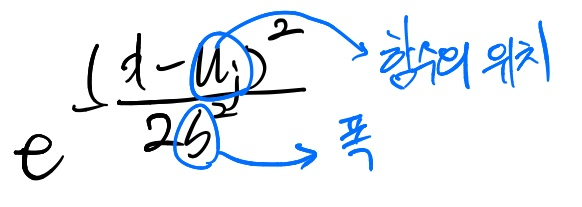
가우시안 기저함수(Gaussian Basis Functions)

가우시안 기저함수는 사이킷런에 함수로 존재하지 않지만 직접 구현할만하다고 한다

규제화(Regularization)

기저함수를 사용함으로써 복잡한 데이터를 모델링할 수 있게 되었지만 과대적합이 될수도 있음

각각의 가우시안 기저함수의 크기(계수값)를 확인해보고 큰 계수값에 penalty를 부여해서 과대적합 극복

가장 많이 사용하는 규제화는 Ridge regression(L2 Regularization)와 Lasso regression(L1 Regularization), SGD

Ridge Regression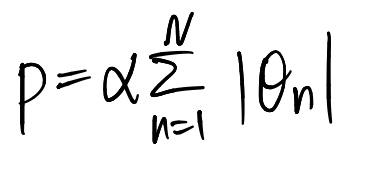

Rasso regression

Rasso regression을 사용하면 sparse한 모델이 생성됨(많은 계수들이 0이 된다)