교육/프로그래머스 인공지능 데브코스
[6주차 - Day4] ML_basics - Linear Algebra
zzangyeah
2021. 6. 4. 17:52
728x90
뗴잉 수학싫어잉
1. 기본표기법(Basic Notation)





import numpy as np
x=np.array([1.2,3.4,5.6,7.8])
x.shape
#>>(4,) 1차원 배열
x
#>>array([1.2, 3.4, 5.6, 7.8])
i=2
x[i]
#>>5.6
#차원증가(2차원 배열)
np.expand_dims(x,axis=1).shape
#>>(4,1)
np.expand_dims(x,axis=1)
'''
>>array([[1.2],
[3.4],
[5.6],
[7.8]])
'''
A=np.array([
[10,20,30],
[40,50,60]
])
A
'''
>>array([[10, 20, 30],
[40, 50, 60]])
'''
A.shape
#>>(2,3)
i=0
j=2
A[i,j]
#>>30
#Column Vector
j=1
A[:,j]
#>>array([20, 50])
#Row Vector
i=1
A[i,:]
#>>array([40, 50, 60])
2. 행렬의 곱셈(Matrix Multiplication)

1. 벡터*벡터(Vector-Vector Products)
내외적 정의 : https://wikidocs.net/22384

import numpy as np
x=np.array([1,2,3])
y=np.array([4,5,6])
x.dot(y)
#>>32
y.dot(x)
#>>32
x=np.expand_dims(x,axis=1)
y=np.expand_dims(y,axis=0)
x.shape, y.shape
#>>((3,1),(1,3))
np.matmul(x,y)
'''
>>array([[ 4, 5, 6],
[ 8, 10, 12],
[12, 15, 18]])
'''외적이 유용한 경우
아래 행렬 A는 모든 열들이 동일한 벡터 x를 가지고 있음 외적을 이용하면 간편하게 나타낼 수 있다

#column vector
x=np.expand_dims(np.array([1,2,3]),axis=1)
x
'''
>>array([[1],
[2],
[3]])
'''
ones=np.ones([1,4]) #ones()원소가 모두 1인 행렬반환
ones
#>>array([[1., 1., 1., 1.]])
A=np.matmul(x,ones)
A
'''
>>array([[1., 1., 1., 1.],
[2., 2., 2., 2.],
[3., 3., 3., 3.]])
'''2. 행렬*벡터(Matrix-Vector Products)
열벡터를 오른쪽에 곱하고 A가 행의 형태로 표현

A=np.array([
[1,2,3],
[4,5,6]
])
A
'''
>>array([[1, 2, 3],
[4, 5, 6]])
'''
ones=np.ones([3,1])
ones
'''
>>array([[1.],
[1.],
[1.]])
'''
np.matmul(A, ones)
'''
>>array([[ 6.],
[15.]])
'''열벡터를 오른쪽에 곱하고 A가 열의 형태로 표현
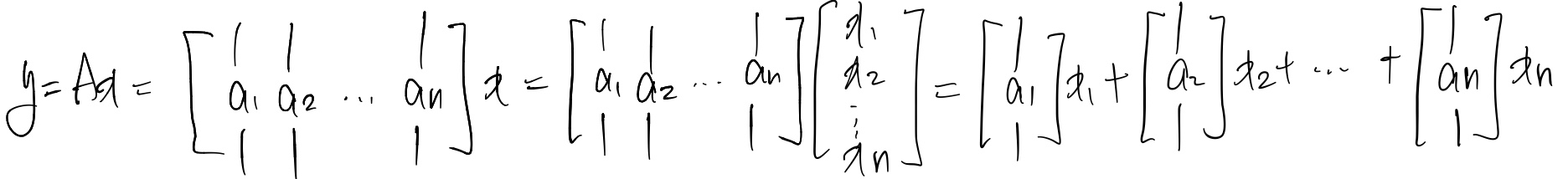
A=np.array([
[1,0,1],
[0,1,1]
])
x=np.array([
[1],
[2],
[3]
])
np.matmul(A,x)
'''
>>array([[4],
[5]])
'''
for i in range(A.shape[1]):
print('a_'+str(i)+':',A[:,i],'x_'+str(i)+':',x[i],
'a_'+str(i)+'*x_'+str(i)+':',A[:,i]*x[i])
'''
>>a_0: [1 0] x_0: [1] a_0*x_0: [1 0]
a_1: [0 1] x_1: [2] a_1*x_1: [0 2]
a_2: [1 1] x_2: [3] a_2*x_2: [3 3]
'''행벡터를 왼쪽에 곱하고 A가 열의 형태로 표현
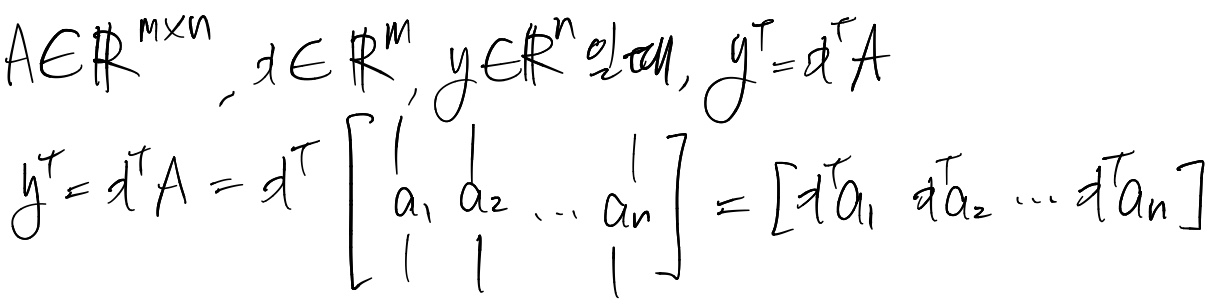
행벡터를 왼쪽에 곱하고 A가 행의 형태로 표현

3. 행렬*행렬(Matrix-Matrix Products)
일련의 벡터*벡터 연산으로 표현하는 경우
1. A가 행으로 B가 열로 표현

2. A가 열로 B가 행으로 표현

일련의 행렬*벡터 연산으로 표현하는 경우
1. B가 열로 표현

2. A가 행으로 표현

3. 중요 연산과 성질들(Operations and Properties)
1. 정방(Square), 삼각(Triangular), 대각(diagonal), 단위(identity) 행렬들
- 정방행렬(square matrix) : 행과 열의 개수가 동일
- 삼각행렬(triangualr matrix)
- 상삼각행렬(upper triangular matrix) : 정방행렬이며 주 대각선 아래 원소들이 모두 0
- 하삼각행렬(lower triangular matrix) : 정방행렬이며 주 대각선 위 원소들이 모두 0
- 대각행렬(diagonal matrix) : 정방행렬이며 주대각선 제외 모든 원소가 0
- 단위행렬(identity matrix) : 대각행렬이며 주대각선 원소들이 모두 1 I로 표시
#대각행렬
#diag()를 사용해서 대각행렬 생성가능
np.diag([4,5,6])
'''
>>
array([[4, 0, 0],
[0, 5, 0],
[0, 0, 6]])
'''
#diag함수에 행렬을 전달하면 주대각선 값들을 얻을 수 있음
D=np.array([
[1,2,3],
[4,5,6],
[7,8,9]
])
np.diag(D)
'''
>>array([1, 5, 9])
'''#단위행렬
#eye()를 사용하면 원하는 크기의 단위행렬 생성가능
np.eye(3)
'''
>>
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
'''2. 전치(Transpose)
행렬을 전치하는 것=행렬을 뒤집는 것

다음의 성질들이 성립

#T속성을 사용해서 전치행렬을 구할 수 있음
A=np.array([
[1,2,3],
[4,5,6]
])
A.T
'''
>>
array([[1, 4],
[2, 5],
[3, 6]])
'''3. 대칭행렬(Symmetic Matrices)
정방행렬 A가 A의 전치행렬과 동일할 때 대칭행렬이라고 함
정방행렬 A가 -(A의 전치행렬)과 동일할 때 반대칭행렬(anti-symmetric matrices)이라고 함
- 정방행렬*정방행렬의 전치행렬=항상 대칭행렬
- 정방행렬+정방행렬의 전치행렬=대칭
- 정방행렬-정방행렬의 전치행렬=반대칭
